Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 27

Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 3 em torno de O A .

Passo 1

O volume gerado pela rotação de uma região pode ser calculado através da seguinte expressão:

V = ∫ a b A ( x ) d x

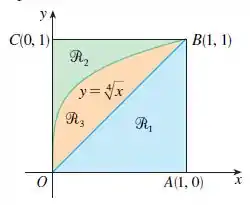
Na nossa questão, queremos saber o volume gerado pela rotação da região R 3 , que é delimitada pela função y = x 4   e y = x . Esse volume é calculado pelo método dos discos, onde temos várias circunferências sendo criadas ao longo do eixo de rotação. No nosso caso, estamos rotacionando a área em torno da reta y = 0 . Assim, a área do disco é igual a:

A x = π R 2 - π r 2 = π x 4 2 - x 2 = π x 1 2 - x 2

Passo 2

Galerinha, vamos primeiro achar o valor dessa integral indefinida e depois aplicamos o Teorema Fundamental do Cálculo para aplicar os limites de integração. Assim, usando duas expressões da Tabela de Integrais Indefinidas:

∫ c f ( x ) d x = c ∫ f ( x ) d x

∫ x n d x = x n + 1 n + 1   + C

Logo,

∫ π x 1 2 - x 2 d x = π ∫ x 1 2 - x 2 d x = π 2 x 3 2 3 - x 3 3 + C

Passo 3

Agora é tranquilo, pessoal! Para achar o volume basta resolver aquela integral apresentada no início do Passo 1. Nossos limites de integração aqui serão a = 0 e b = 1 pois são os pontos que delimitam a nossa região de trabalho. Assim, fazendo uso do Teorema Fundamental do Cálculo:

V = ∫ 0 1 x 1 2 - x 2 d x = π 2 x 3 2 3 - x 3 3 0 1

V = π 2 3 - 1 3 = π 3

Resposta

O resultado final é:

V = π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

43. A base de um sólido é a região encerrada por um círculo com 7 cm de raio. Ache o volume do sólido se todas as secções planas perpendiculares a um diâmetro fixo da base forem triângulos equiláteros
42. A base de um sólido é a região encerrada por um círculo com 2 unidades de raio. Ache o volume do sólido se todas as secções planas perpendiculares a um diâmetro fixo da base forem quadradados.
41. Um sólido de revolução é formado pela rotação, em torno do eixo x, da curva limitada pela curva y = 2 x + 4 , pelo eixo x, pelo eixo y, e pela reta x=c (c0). Para que valor de c o volume será de 1
46. A base de um sólido é a região encerrada por um círculocom um raio de r unidades, e todas as secções planas perpendiculares a um diâmetro fixo da base são triângulos retângulos isósceles, com a hi
45. A base de um sólido é a região a região do Exercício 43. Ache o volume do sólido se todas as secções planas perpendiculares a um diâmetro fixo da base forem triângulos isósceles de altura igual à