Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 36
36. Um tanque de óleo na foma de uma esfera tem um diâmetro de 18m. Quanto óleo o tanque contém se a profundidade do óleo é de 7m?
Passo 1
O diâmetro é 18, então, o raio é 9, pois .
Podemos observar a seguinte relação:
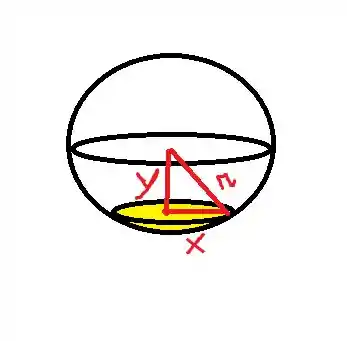
Por Pitágoras, o raio do disco amarelo é dado por
Então, a área desse mesmo disco será dado por
Passo 2
A integral ficará assim:
Resposta
Exercícios de Livros Relacionados
Determinar o volume do sólido de revolução gerado pela rotação das regiões indicadas, ao redor dos eixos dados. y = x 2 3 e y = 4 ; ao redor dos eixos x = - 9 , y = 0 e x = 0
Calcular o volume do sólido gerado pela rotação, em torno da reta y = 2 , da região limitada por y = 3 + x 2 , x = - 2 , x = 2 e y = 2
Encontrar o volume do solido gerado pela rotação, em torno do eixo dos x , da região limitada por y 2 = 16 x e y = 4 x .
Calcular o volume do sólido gerado pela rotação, em torno da reta y = 2 , da região limitada por y = 1 - x 2 , x = - 2 , x = 2 e y = 2
Determinar o volume do sólido de revolução gerado pela rotação das regiões indicadas, ao redor dos eixos dados. y = x + x 2 e y = x 2 - 1 ; ao redor do eixo y = 1