Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.4 - Ex. 27
A velocidade de disparo de uma arma é de . Determine dois ângulos de elevação que podem ser utilizados para atingir um alvo que está a de distância.
Passo 1
Olá, tudo bem? Bom... o enunciado quer que calculamos dois ângulos de elevação que podem ser utilizados para atingir um alvo que está a de distância utilizando uma arma que tem velocidade de disparo .
Para isso, vamos imaginar aqui como será o movimento da bala do disparo até o alvo:
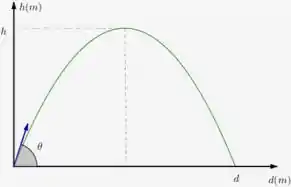
Os dados iniciais são:
- Velocidade inicial:
- Ângulo de elevação:
- Aceleração da gravidade:
- Vetor posição inicial:
Obs: temos esse vetor de posição inicial dessa forma pois estamos partindo da origem.
Com isso, vamos montar o vetor posição em função do tempo para encontrarmos os ângulos.
Ahhh, vamos calcular a velocidade inicial da componente vertical e horizontal da bola (pois a gente vai precisar rsrs):
- Vertical:
- Horizontal:
Passo 2
Agora podemos montar o vetor posição em função do tempo .
Mesclando o conceito que vimos na Física com esse conteúdo de funções vetoriais, podemos fazer:
Substituindo as componentes:
Beleza até aqui?
Passo 3
Agora vamos pensar um pouco...
O tempo que a bola leva para percorrer, na horizontal, a distância de não é o mesmo tempo que a bola leva para subir e descer? É SIM! Então, da componente vertical, vamos descobrir o tempo de voo.
Ou seja, aquele instante no qual a componente é zero:
Como o instante é:
Simplificando e isolando :
E agora substituir na componente horizontal essa quantidade, porque assim vamos ficar com uma expressão do ângulo em função do alcance de , sacou?
Passo 4
Beleza! Vamos às substituições!
Pegando a componente vertical da posição em função do tempo:
E substituindo pelo tempo temos:
E reorganizando um pouco teremos:
E podemos simplificar um pouco mais se usarmos a relação trigonométrica :
Passo 5
Sabendo que o alcance foi de , temos:
O outro valor de é quando lançamos a bola para o outro sentido do eixo horizontal.
Ou seja, quando o ângulo é , temos:
Então os dois ângulos possíveis são: .