Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 19
Verificar que a curva:
É a metade de uma hipérbole. Encontrar a equação cartesiana.
Passo 1
Então galera, a curva que nos foi dada é uma função vetorial, então já está parametrizada em termos de . No entanto, como é vetorial, então possui componentes em e em , certo? Pela curva que nos foi dada, temos que a parametrização é:
Até aqui tudo certo, não é? OK! A estratégia que vamos utilizar para determinar a equação cartesiana da curva será: como e estão escritos em termos de seno e cosseno hiperbólico, vamos utilizar a relação fundamental da trigonometria hiperbólico para escrever tudo em uma expressão só, tudo bem? A relação é:
Sabendo disso, então bora pra cima agora!
Passo 2
Se elevarmos ao quadrado, teremos:
Se elevarmos ao quadrado, teremos:
Multiplicando a primeira equação por e a segunda equação por , teremos:
Substituindo na relação fundamental da trigonometria hiperbólico, teremos:
Pela equação que encontramos, fica claro concluir que se trata de uma hipérbole! Agora nos resta provar que se trata da METADE de uma hipérbole.
Passo 3
Então pessoal, assim como sabemos, temos que , certo? Em termos de componente, ou seja, utilizando a parametrização, temos que:
Sendo assim, pela definição acima, teremos:
Sabendo que uma hipérbole é simétrica em relação ao eixo , como temos uma restrição para a função, isso implica que teremos apenas uma parte da hipérbole, assim como mostrado no gráfico abaixo:
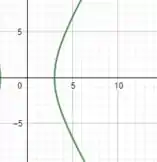
E está aí nossa demonstração! 😉
Resposta
Equação cartesiana: