Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 2
Seja .
- Representar graficamente o conjunto , identificando se é aberto.
- Determinar a fronteira de .
Passo 1
a) Vamos começar representando o conjunto graficamente. Pensa um pouquinho no que ele representa. Tá vendo essa desigualdade no ? Isso aí representa todo o espaço entre as retas e . Ao mesmo tempo, pro , representa todo o espaço entre e . Isso vai ficar assim:
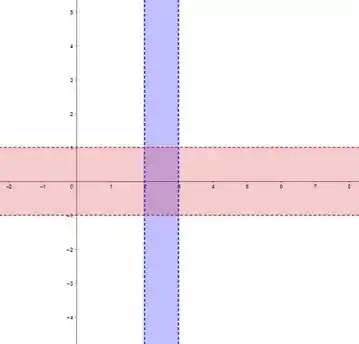
Só que o que a gente tá interessado é na interseção desses conjuntos!
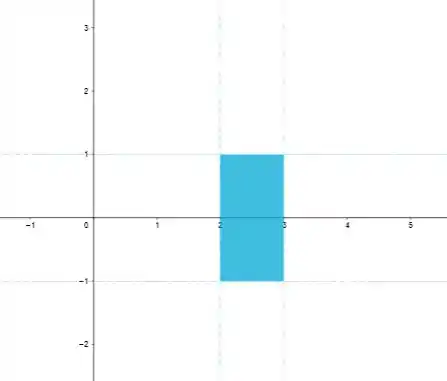
Como esse conjunto tem as bordinhas todas abertas, por causa das inequações, ele é um conjunto aberto.
Passo 2
b) A fronteira de é esse retângulo que foi formado aí. Os vértices dele podem ser determinados interceptando as retas, ou basta olhar pro gráfico! Dali do desenho nós podemos ver que os pontos são:
Resposta
- O conjunto é aberto.
- Retângulo de vértices , , , .
Exercícios de Livros Relacionados
Encontrar uma função de várias variáveis que nos dê:d) A quantidade, em metros quadrados, de papel de parede necessária para revestir as paredes laterais de um quarto retangular de x metros de largura
Determinar o domínio e o conjunto imagem das seguintes funções:e) f x , y , z = x 2 + y 2 + z 2
Determinar o domínio e o conjunto imagem das seguintes funções:d) w = e x 2 + y 2 + z 2
Determinar o domínio e o conjunto imagem das seguintes funções:j) f x , y = 4 - x 2 - y 2
Determinar o domínio e o conjunto imagem das seguintes funções:g) z = x 2 + y 2 - 2