Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas da grade que têm constante e quais têm constante.
Passo 1
Fala ai gente . O exercício está pedindo para a gente plotar o gráfico da superfície parametrizada de:
Onde:
e determinar quais serão as curvas de grade que têm constante e quais têm constante.
Primeiro passo que vamos fazer é achar os valores correspondentes a e e depois plotar o gráfico em um software.
Depois iremos analisar as curvas de grade vendo comomanipular as equações ficam considerandocom constante e comou constantes, e ver que tipo de função a gente encontra..
Partiu!
Passo 2
Primeiro então vamos achar os valores de . Sabemos que :
Então:
Plotando em uma calculadora gráfica 3D, a superfície parametrizada é:
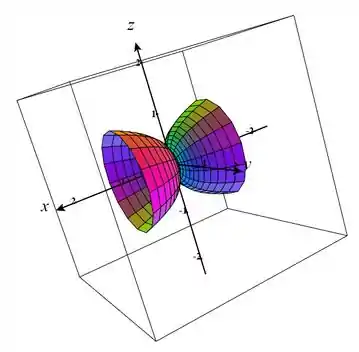
Passo 3
Agora vamos fazer com que seja constante, mas antes vamos tentar achar uma relação entre as equações.
Se elevarmos as equações de e ao quadrado e somarmos :
+
teremos que:
Sabemos que .
E como aqui a gente tá considerando constante, essa equação aí é bem parecida com a de uma circunferência:
Então as equações descrevem uma circunferência no plano de raio . Assim, a curva correspondente são circunferências paralelas ao plano .
Pra cada valor de , pra cada valor de a circunferência vai ter um raio diferente.
Podemos representar um deles graficamente:
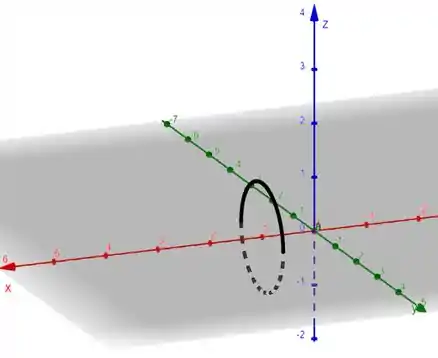
Passo 4
Agora vamos ver como fica a curva quando é constante:
Vamos dividir a segunda equação pela terceira:
Mas como é uma constante, então a sua tangente também vai ser constante. Vamos reescrever assim:
E finalmente isso tá com uma cada mais conhecidinha. Isso é uma reta ne, o que significa que nos planos paralelos ao plano , nós vamos ter retas com inclinação .
Hmmm mas e a variável ???
Bom, como e , nós temos:
Substituindo em :
Mas lembre-se novamente que é constante, então seu seno e cosseno também vão ser. A gente vai inventar aqui duas constantes novas, mas não se assusta, é só pra você ver que essas equações são mais familiares do que você pensa:
Ta vendo, é apenas um polinômio de grau 3 e o seu comportamento já é bem conhecido.
Então concluímos finalmente que, quando é constante, a gente vai ter polinômios de grau 3, nos planos e .
escrever tudo em função de
Logo:
Assim, essas são as curvas que estão nos planos que passam pelo eixo .
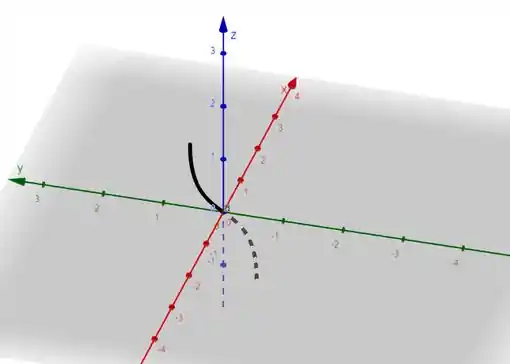
Resposta
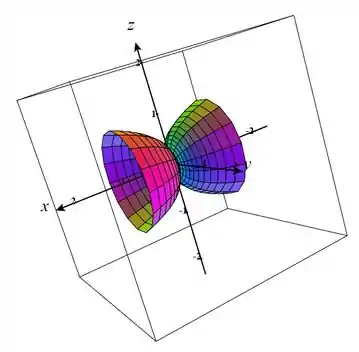
constante são circunferências paralelas ao plano .
v constante são correspondentes às curvas que estão nos planos que passam pelo eixo .