Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 32
Os vértices opostos de um quadrado estão em e . Ache os outros dois vértices.
Passo 1
Para isso, precisamos lembrar que a diagonal do quadrado mede vezes o lado, que o centro do quadrado divide as duas diagonais ao meio e que o ponto médio de um segmento de reta com extremidades e é dado por
Passo 2
Como temos dois vértices opostos, podemos calcular qual é o centro do quadrado:
Passo 3
Como as diagonais do quadrado são perpendiculares e os vértices opostos dados possuem a mesma ordenada, os vértices opostos que queremos encontrar possuem a mesma abcsissa entre si e com o centro, ou seja, estão sobre a reta verde abaixo:
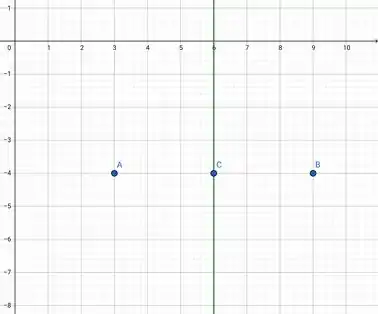
Passo 4
Pelos passos anteriores, podemos facilmente notar que a distância do centro para os dois vértices dados é igual a três unidades e, como as diagonais de um quadrado são iguais, os vértices buscados estão à mesma distância do centro. E como já sabemos a abscissa dos dois vértices, temos que eles são e .