Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 134
Calcule a excentricidade de uma elipse, sabendo que as extremidades das cordas que contêm algum foco e são perpendiculares ao eixo maior são vértices de um quadrado inscrito na elipse.
Passo 1
Suponha que temos a elipse .
Temos o seguinte esquema:
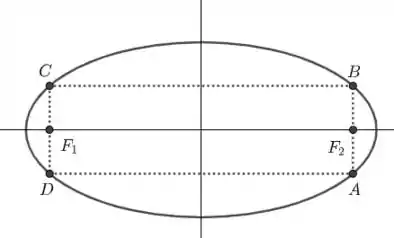
Seja um ponto da elipse. Logo:
Passo 2
Mas é um quadrado. Assim, temos que :
Passo 3
Assim, para descobrirmos o valor de , basta resolver a equação do 2° grau:
Como , devemos aceitar apenas a raiz positiva:
Resposta
O valor da excentricidade é .
Exercícios de Livros Relacionados
Para as funções dadas f e g defina f + g e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4
Para as funções dadas f e g defina f / g e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4
Para as funções dadas f e g defina g / f e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4
Para as funções dadas f e g defina g / f e determine o domínio da função resultante. f x = x e g x = 1 x 2
Para as funções dadas f e g defina g / f e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3