Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 13
Se você tiver um sca que possa calcular aproximações usando pontos médios e esboçar os retângulos correspondentes (use os comando RiemannSum ou middlesum e middlebox no Maple), verifique a resposta do Exercício 11 e ilustre com um gráfico. Repita então com e .
Passo 1
Pessoal, nessa questão vamos usar uma calculadora programável para verificar a resposta do Exercício que é:
Usando para a regra do Ponto Médio.
Devemos verificar a resposta e também devemos plotar o gráfico da função e dos retângulos obtidos.
Por fim, vamos repetir usando um maior de subintervalos. e .
A regra do ponto médio é uma soma de Riemann que utiliza os valores de de cada subintervalo escolhidos no ponto médio do subintervalo.
A soma de Riemann é calculada com valores de escolhidos dentro de subintervalos.
Ela representa a soma das áreas de retângulos que são obtidos a partir da função.
A ideia é basicamente dividir o intervalo em subintervalos igualmente espaçados.
Esses serão as bases dos retângulos.
Para a altura do retângulo, pega-se o valor da função em um ponto dentro do subintervalo .
Como estamos usando a regra do ponto médio, o valor de é o ponto médio de cada subintervalo.
Passo 2
Vamos verificar o exercício 11. Ou seja, usar as aproximações com pontos médios para
A integral é:
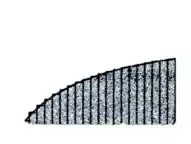
Usando a calculadora programável (ela já possui funções próprias para isso, por exemplo, os comando RiemannSum ou middlesum e middlebox no Maple). Usando temos a seguinte resposta:
Ilustrando,
Já para , temos que
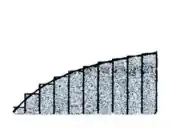
E para
