Operações com matrizes
Produzido por Marcelo LuizTeoria
Soma e subtração
Caara, chegamos na parte de fazer as operações com as famosas matrizes. Vamos começar com a soma e subtração
Exemplo :
A ideia é você somar (ou subtrair )elemento com elemento, ou seja, primeiro termo de uma matriz com o primeiro termo da outra e assim vai, dessa forma :
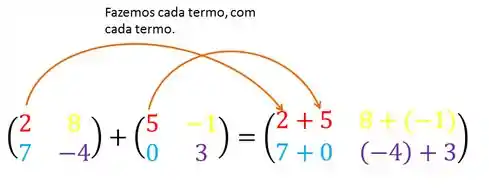
Agora é só terminar, fazendo essas continhas:
Então a ideia é essa para soma e subtrações de matrizes. Única coisa que você tem que tomar cuidado é que para você somar as matrizes ambas tem que ter a mesma quantidade de linhas e colunas .
Multiplicação por escalar
Fazer a multiplicação de uma matriz por um escalar é bem tranquilo, basta você multiplicar todos os termos da matriz por esse escalar, ou seja ele entra para dentro da matriz multiplicando todos os elementos :
Ex :
O escalar vai entrar na matriz multiplicando cada termo:
Prontinho, a ideia é a mesma para qualquer que seja a quantidade de linhas e colunas da nossa matriz.
Multiplicação entre matrizes
Para resolver a multiplicação entre duas matrizes ( A e B) você precisa que isso aconteça :
O número de colunas da matriz A têm que ser igual ao número de linhas da matriz B, nesse caso ambas são n. E o resultado sempre vai ser a quantidade de linhas da primeira e a quantidade de colunas da segunda.
CUIDADO:No caso das matrizes
Então você sempre vai ter que cuidar esse lance do número de colunas da primeira matriz ser igual ao número de linhas da segunda.
Beleza, mas como resolver essa multiplicação?
Grava essa frase aqui:
“Linha por coluna”
Quando você pegar duas matrizes se multiplicando você fixar a primeira linha da matriz A e multiplica primeiro pela primeira coluna da matriz B, depois a segunda, até acabar as colunas da matriz B. Assim, você vai estar calculando cada um dos termos da nossa matriz resultada da multiplicação.
Depois passamos para as outras linhas da matriz A, sempre repetindo o mesmo procedimento. Até acabar a matriz toda.
Ex:
Vamos calcular , da uma olhada que a matriz A tem 2 colunas e a matriz B tem 2 linhas, e por elas serem iguais, podemos multiplicar:
Vamos multiplicar a primeira linha da matriz A com a primeira coluna da matriz B:
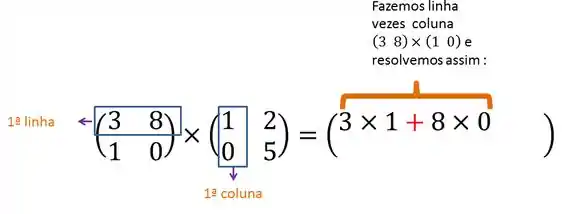
Agora continuando na primeira linha da matriz A, vamos multiplicar a segunda coluna de B:
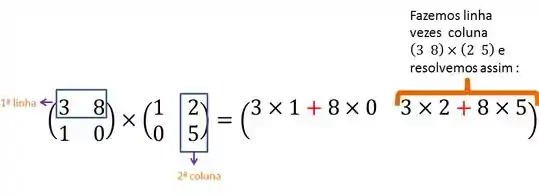
Terminamos a primeira linha, vamos para a segunda e a primeira coluna novamente :
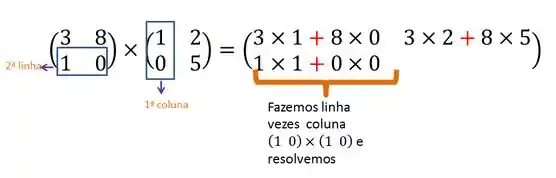
Para finalizar vamos pegar a segunda coluna:
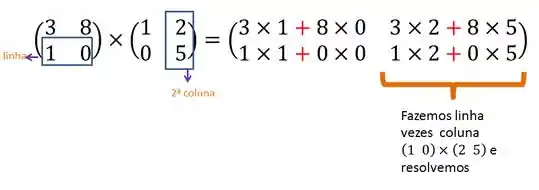
Agora é só resolver a expressãozinha pra cada termo, e no final ficamos por resultado :
É ISSO GALERAAA, bora exercicios
Multiplicação por escalar
Multiplicação entre matrizes
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração propria
Faça a soma :
Passo 1
Para fazer essa conta, não podemos esquecer que em soma de matrizes, é feito elemento com elemento.
Ou seja, com e e assim por diante.

Aggora é só somar, e teremos :
Resposta
Exercício Resolvido #2
Elaboração propria
Resolva :
Passo 1
Subtrair é a mesma ideia da soma, nós faremos elemento por elemento:
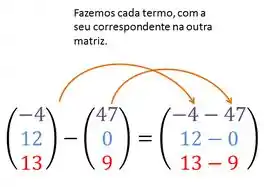
Agora , fazendo essas subtrações, temos :
Resposta
Exercício Resolvido #3
Elaboração Própria
Dado calcule:
Passo 1
Quando temos a multiplicação de um escalar por uma matriz, fazemos o escalar vezes cada um dos elementos da matriz,
Fizemos o escalar entrar dentro da nossa matriz multiplicando todos os termos, agora é só resolver:
Passo 2
Novamente, temos uma multiplicação:
Resolvendo:
Resposta
Exercício Resolvido #4
Elaboração Própria
Sejam e , calcule:
Passo 1
Para começar, vamos fazer a multiplicação de cada raiz por seu escalar e no final fazemos a soma.
Primeiro:
Na multiplicação por escalar, podemos jogar ele para dentro multiplicando todos os termos:
Passo 2
Agora, vamos para a segunda matriz:
Novamente podemos jogar o escalar para dentro multiplicando:
Passo 3
Agora é só fazer a soma:
Na soma, fazemos cada termo com o céu correspondente na outra matriz, assim ficamos com:
Resposta
Exercício Resolvido #5
Elaboração Própria
Sejam , e , calcule:
Passo 1
Podemos fazer a subtração primeiro e depois a soma:
Então, vamos começar a calcular:
Passo 2
Antes de descobrir quanto vale a soma, precisamos do valor de:
Como é uma multiplicação por escalar, ele entra dentro da matriz multiplicando os termos:
Passo 3
Agora é só juntar:
Resposta
Exercício Resolvido #6
Elaboração própria
É possível fazer as seguintes multiplicações?
Passo 1
Para começarmos precisamos lembrar que para multiplicar duas matrizes, é preciso que: o número de colunas da primeira matriz seja igual ao número de linhas da segunda.
a)
Vamos começar contando o número de colunas da primeira matriz, podemos ver que ela tem duas.
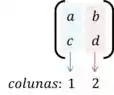
Agora vamos contar o número de linhas da segunda matriz, podemos observar facilmente que ela possui duas linhas.
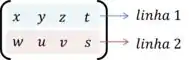
Como a quantidade de colunas da primeira matriz é igual a de linhas da segunda matriz, podemos fazer essa multiplicação.
Passo 2
b)
Seguindo a mesma ideia, a primeira matriz é igual a da letra a do exercício e possui 2 colunas.
Só que agora a segunda matriz possui 3 linhas.
Como esses valores são diferentes, não podemos realizar essa multiplicação.
Resposta
- Sim
- Não
Exercício Resolvido #7
Elaboração própria
Seja a matriz
Calcule
Passo 1
Vamos lembrar que , ou seja, vamos calcular:
Para multiplicar duas matrizes, vamos lembrar-nos da nossa frase: “Linha por coluna”.
Vamos fixar a primeira linha da primeira matriz, e vamos multiplicar pela primeira coluna para descobrir o nosso primeiro elemento.

Continuando com a primeira linha fixada, vamos multiplicar pela segunda coluna:
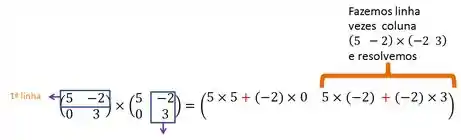
Passo 2
Agora, fixamos a segunda linha e multiplicamos pela primeira coluna:

Agora a segunda linha, com aa segunda coluna:
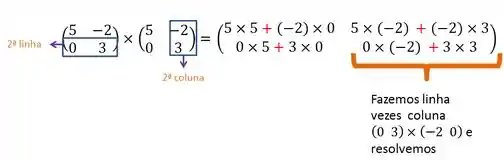
Passo 3
Assim, temos:
Resposta
Exercício Resolvido #8
Elaboração própria
Calcule:
Passo 1
Para resolver a multiplicação, fixamos uma linha e multiplicamos pela primeira, depois a segunda e por fim a terceira coluna da nossa segunda matriz.
Então, vamos fixar a primeira linha e multiplicar pela
- Primeira coluna
- Segunda coluna
- Terceira coluna
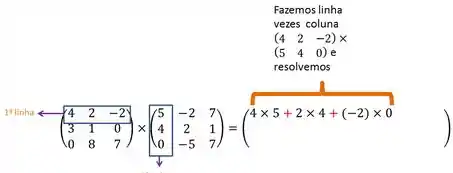
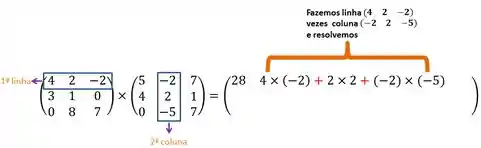

Passo 2
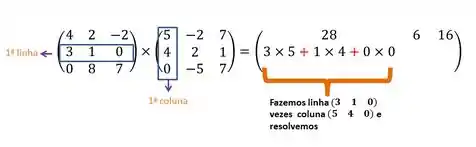
Agora, fixamos a segunda linha e fazemos o mesmo
- Primeira coluna
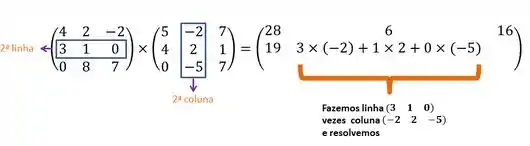
- Segunda Coluna
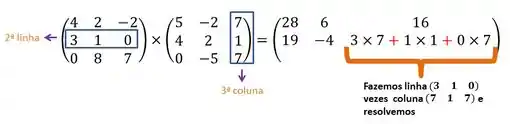
- Terceira Coluna
Passo 3
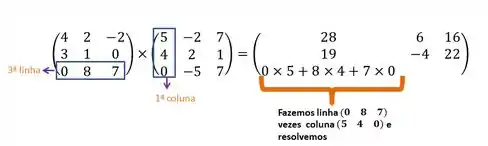
Agora fixamos a terceira linha
- Primeira coluna
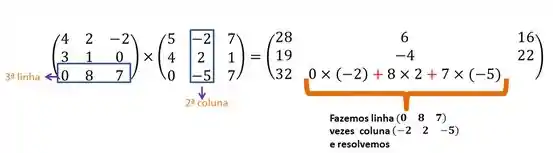
- Segunda coluna
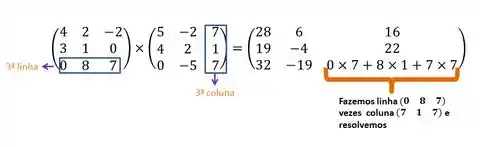
- Terceira coluna
Passo 4
Assim,