Operações com vetores
Teoria
Soma entre vetores- regra do paralelogramo
Fala minha genteee, já vimos o que é um vetor, e agora vamos ver algumas operações que podemos fazer com eles.
Para a soma, temos duas opções:
- Regra do paralelogramo
- Fechamento do triângulo
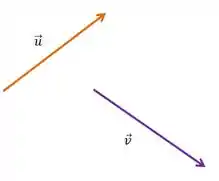
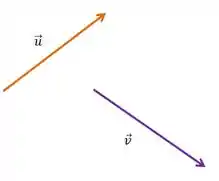
Vamos começar, imagine dois vetores:
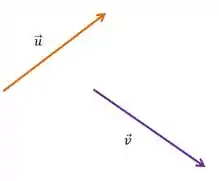
E você quer fazer a soma deles, tá MAS COMO ?
Primeiro vamos usar a regra do paralelogramo:
A ideia é a seguinte, primeiro você vai colocar os vetores saindo de uma mesma origem. Lembrando que se não mudarmos nem o módulo, nem a direção e nem o sentido de um vetor, ele continua sendo igual.
Então, vamos arrastar os vetores para deixar eles com a mesma origem, lembrando-se de não mudar nenhuma das características do vetor que queremos (basicamente só vamos “desenhar” ele em outro lugar).
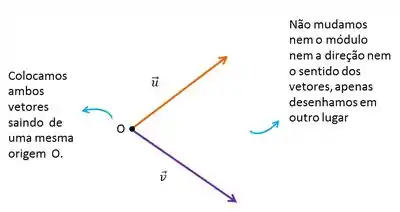
Feito isso, agora vamos fazer uma reta tracejada paralela ao vetor , que começa na extremidade do vetor
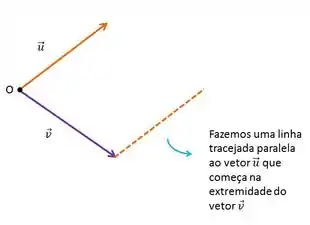
Agora, também fazemos uma linha tracejada, mas agora paralelo ao vetor , e que começa na extremidade do vetor :
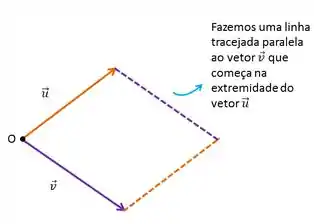
Essa figura que acabamos de formar é um paralelogramo, é por isso que tem esse nome hahaha.
A soma desses vetores é a reta que começa na origem O e termina no encontro das linhas tracejadas:
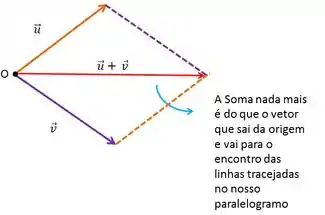
E nesse caso, se quisermos saber o valor do módulo (comprimento) da soma, vamos usar essa formulazinha aqui (vamos chamar o vetor de ):
Onde:
R é o módulo da soma
u e v são os módulos de cada um dos vetores.
é o ângulo entre os vetores u e v (quando ambos estão na mesma origem).
EX:
Dois vetores têm direções perpendiculares, com módulo 3 e com módulo 5, calcule o vetor resultante :
Pela regra do paralelogramo, vamos usar a fórmula
Onde temos :
ou perpendicular.
Como temos que ,
Prontinho então a regra do paralelogramo tem os seguintes passos;
1º Colocar os vetores saindo de uma mesma origem
2º Fazer as linhas tracejadas
3º Encontrar o vetor correspondente a soma
Soma entre vetores- regra do fechamento do triangulo
A segunda maneira de resolver é por meio do fechamento do triangulo:
Vamos usar os mesmos vetores
Agora ao invés de colocar ambos saindo de uma mesma origem, vamos colocar um dos vetores saindo da extremidade do outro:
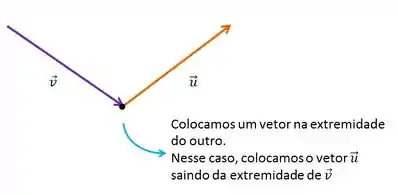
Se quisermos colocar o vetor na extremidade do , também da certo.
Feito isso a soma é o vetor que começa na origem do primeiro vetor e que termina na extremidade do ultimo, ou seja,
:
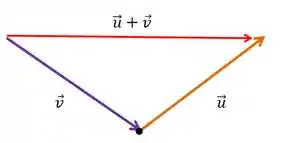Nós realmente fechamos para formar um triangulo.
Se quisermos saber o módulo da soma usamos :
Onde :
R é o módulo da soma
u e v são os módulos de cada um dos vetores.
é o ângulo entre os vetores u e v.
Subtração entre vetores:
Agora, queremos subtrair os vetores:
Ou seja, queremos saber quanto é , para resolver temos que lembrar que
É o vetor oposto de , ou seja, eles têm mesmo módulos e direção, mas sentidos contrários.
Assim basta vermos essa diferença como uma soma:
Ai é só inverter a direção da seta do vetor no desenho, e depois é só resolver a soma.
Multiplicação por um escalar:
Um escalar é um número qualquer que estamos acostumados ( 1, 8, -7 ...)
Quando multiplicamos um vetor por um escalar, ele apenas vai mudar seu tamanho e o resultado do módulo vai ser o escalar multiplicado do módulo do próprio vetor.
Ex:
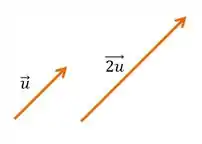
Ou seja, se temos um vetor , e queremos multiplica-lo por 2. Nós fazemos ele com o dobro do seu tamanho. E seguimos essa ideia para todo escalar.
E se for dado o valor do módulo vetor e quiser saber o valor do resultado do módulo de, vamos simplesmente multiplicar o módulo pelo escalar.
Por exemplo:
É isso, partiu exercíciosss ^~^
Soma entre vetores- regra do fechamento do triangulo
Subtração entre vetores:
Multiplicação por um escalar:
Exercícios Resolvidos
Exercício Resolvido #1
CHIQUETTTO, Marcos José;Física São Paulo, SP: Spicione, 2000. pp.50
Dois vetores e têm direções perpendiculares. Seus módulos são e . Determine o módulo da soma
Passo 1
Como temos direções perpendiculares, temos algo mais ou menos assim:
E pela regra do paralelogramo a soma tem módulo:
E é o valor do ângulo entre eles, por estarem perpendiculares:
Passo 2
Resolvendo, temos:
Resposta
10
Exercício Resolvido #2
CHIQUETTTO, Marcos José; Física São Paulo, SP: Scipione, 2000. pp.50
Obtenha a soma de dois vetores e , de módulos e , sabendo que ele tem a mesma direção e mesmo sentido.
Passo 1
Temos dois vetores de mesma direção e sentido:
A soma é feita com a soma do módulo de cada um;
Resposta
16
Exercício Resolvido #3
Elaboração própria
Se e e estão perpendiculares, calcule o módulo de
Passo 1
Para calcular o resultado, vamos usar essa formulazinha que vem da regra do paralelogramo. Iremos usar essa regra, por que estamos com as origenss ligadas.
E é o valor do ângulo entre eles, por estarem perpendiculares:
Passo 2
Agora é só substituir os valores dados:
Resposta
Exercício Resolvido #4
Elaboração própria.
Sabendo de , calcule o módulo dos seguintes itens:
a)
b)
Passo 1
a)
Temos uma multiplicação por um escalar, nós podemos simplesmente pegar o valor do módulo e multiplicar pelo escalar:
Passo 2
b)
Utilizando a mesma ideia:
Resposta
- 18
- 3
Exercício Resolvido #5
Elaboração própria
Se , e (ângulo entre os vetores e ) , calcule o módulo de
Passo 1
Nesse caso, temos a regra do fechamento o triângulo, uma vez ligando a extremidade de a origem de formamos um triângulo.
Com isso, para calcular o valor da resultante usamos a formulazinha:
Onde, nesse caso temos:
, e
Passo 2
Substituindo os valores:
Resolvendo:
Belezinha ;)
Resposta
Exercício Resolvido #6
CHIQUETTTO, Marcos José;Física São Paulo, SP: Spicione, 2000. pp.50
Obtenha a soma de dois vetores e , de módulos e , sabendo que eles tem a mesma direção e sentidos opostos.
Passo 1
Podemos ver os dois vetores da seguinte forma:
Como temos sentidos opostos, a soma vira subtração dos módulos.
Resposta
4
Exercício Resolvido #7
CHIQUETTTO, Marcos José;Física São Paulo, SP: Spicione, 2000. pp.51
Dois vetores e têm módulos e . Determine o módulo do vetor nos seguintes casos:
- e com a mesma direção e mesmo sentido
- e com a mesma direção e sentidos opostos
Passo 1
- Quando temos a mesma direção e sentido, podemos apenas somar o módulo de cada um dos vetores:
- Quando temos a mesma direção, mas sentidos opostos, podemos apenas diminuir o módulo de cada um dos vetores:
Resposta
- 140
- 60
Exercício Resolvido #8
Elaboração própria
Considere dois vetores: um de módulo e outro de módulo . Mostre como deve ser os vetores para que sua soma tenha módulo:
- 70
- 10
- 50
Passo 1
- Se fizermos um vetor mais o outro:
- Se subtrairmos:
- E se eles forem de direção perpendicular temos:
Mas para poder somar, precisamos de mesma direção e sentido.
Passo 2
Assim, precisamos de vetores na mesma direção e sentidos opostos.
Passo 3
Resposta
- mesma direção e sentido
- mesma direção e sentidos opostos
- direção perpendicular