Inequação

Fala aí, nós somos o Responde Aí, e nossa missão é ajudar você a mandar bem na sua prova.

Eu sei que o assunto é inequação, mas vamos começar rapidinho aqui lembrando da carinha de uma equação:

Quando falamos de equação temos sempre uma igualdade. A inequação é exatamente o oposto, teremos uma DESIGUALDADE e, assim, não aparecerá mais o sinal de igual ($=$), mas sim os sinais de “maior que” ($>$), “maior ou igual que” ($\ge$), “menor que” ($<$) e “menor ou igual que” ($\le$).

Assim como as equações são classificadas em polinomiais, exponenciais e assim por diante, as inequações também são, como por exemplo:

E ainda existem muitas outras classificações para as inequações.

As equações são utilizadas quando queremos saber o zero da função, ou seja, quando queremos saber para qual(is) valor(es) de $x$ a função, $y$, vale zero, não é? Na inequação é um pouco diferente, queremos analisar a função um pouco mais a fundo, queremos saber por exemplo para quais valores de $x$ a função é maior que $4$, ou menor que $0$, sacou?

Vamos fazer um exemplo aqui. Considere essa função polinomial de 1° grau:

Suponha que queremos saber para quais valores de $x$, a função é maior que zero, ou seja, temos que resolver a seguinte inequação:

O gráfico dessa função tem essa carinha aqui:

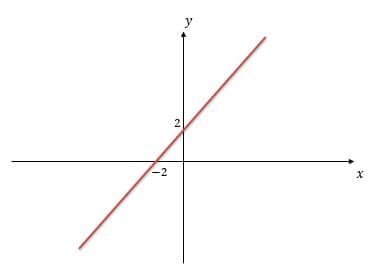
A função assume valor maior que zero, nessa região aqui:

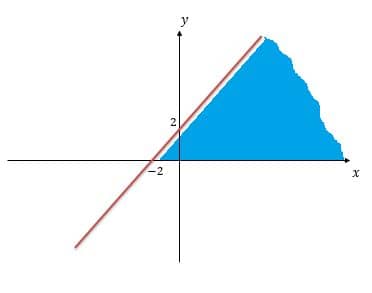
Nós temos que quando $x>-2$, a função assume valores maiores que zero, então essa é a resolução da nossa inequação.

Show de bola né?

Finalizamos por aqui, mas continua aqui com a gente para ter acesso a muito mais conteúdos irados =)