Diagrama de Venn
Resumo
Fala aí, nós somos o Responde Aí, e nossa missão é ajudar você a mandar bem na sua prova. E agora você vai conferir o Diagrama de Venn
O Diagrama de Venn é uma maneira de organizar conjuntos utilizando circunferências. Com ele a gente pode representar as interseções entre conjuntos.
Mas pra que serve o Diagrama de Venn? Com o Diagrama de Venn conseguimos representar de forma mais clara a interseção entre conjuntos e acharmos a união entre eles.
Interpretando o diagrama de Venn
Na maioria dos casos, o diagrama de Venn consistem em três círculos que se cruzam. Cada círculo representa um conjunto, e as áreas de interseção mostram as regiões em que os conjuntos possuem elementos em comum:
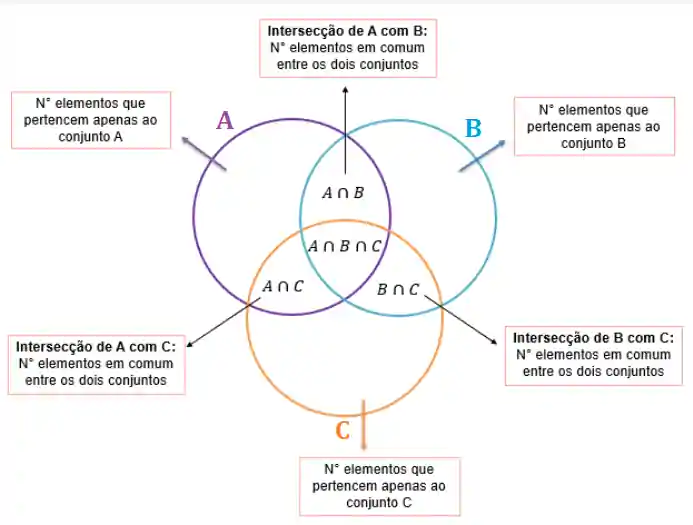
Se quisermos saber a união entre os três conjuntos devemos fazer a seguinte conta:
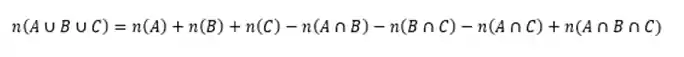
E se quisermos saber a união entres dois conjuntos, fazemos:
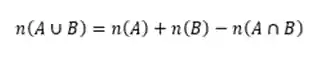
Como resolver problemas com o Diagrama de Venn?
Bora fazer um exemplo pra deixar tudo bem claro!
Exemplo: 200 alunos foram fazer uma prova. A prova tinha 2 questões, apenas 4 alunos acertaram as duas questões, 100 acertaram somente a primeira e 50 acertaram somente a segunda. Construa o Diagrama de Vens e diga quantos alunos erraram as duas questões.
Passo 1: Primeiro, a questão fala que alguns alunos acertaram somente a primeira questão, alguns acertaram somente a segundo, e outros acertaram as duas.
Então vamos desenhar uma bolinha rosa que representa os alunos que acertaram a primeira questão, uma bolinha verde que representa os alunos que acertaram a segunda questão. E a região entre eles representa os alunas que acertaram as duas.
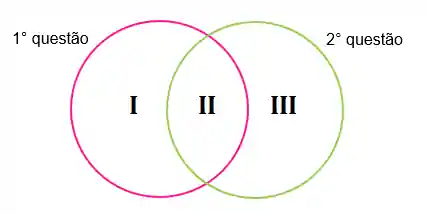
Passo 2: Agora vamos preencher o diagrama.
Na região I vamos colocar a quantidade de alunos que acertaram apenas a primeira questão:
Na região II vamos colocar a quantidade de alunos que acertaram as duas questões:
Na região III vamos colocar a quantidade de alunos que acertaram apenas a segunda questão:
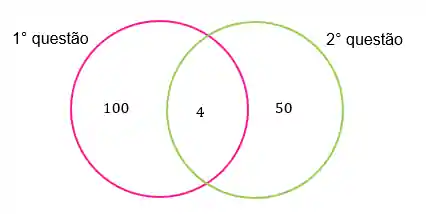
Passo 3: O número de alunos que erraram as duas questões será o número total de alunos (200) menos o número que acertaram a primeira (100), menos o número que acertaram a segunda (50), menos o número que acertaram as duas (4).
Viu como é bacana?!
Quer saber mais? Então da uma olhada aqui no site que tem conteúdo completo das suas matérias mais importantes!