Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Funções Hiperbólicas

Ver Todos os Exercícios

Teoria

Fala aí! Chegou a hora de falar de funções hiperbólicas. Vamos ver que essas funções são aquelas em que aparece o seno ou cosseno hiperbólicos (senh ou cosh).

Vem comigo!

O que é uma função hiperbólica?

Esse tipo de função envolve seno ou cosseno hiperbólico e seus derivados. Eles tem essa carinha aqui:

Só que tem o seguinte, esses caras escondem um segredo sombrio por trás dessa carinha bonitinha. Na verdade, eles são equivalentes a isso aqui:

Como o nome sugere, esses caras aí estão relacionados com hipérboles, ao passo que as funções trigonométricas convencionais, sen(x) e cos(x), estão relacionadas com o círculo trigonométrico.

Expressões das funções hiperbólicas

Aquela relação fundamental trigonométrica também vale pra esses caras aqui, só que a gente vai trocar a soma por uma subtração.

Os parentes tangente, cotangente, secante e cossecante hiperbólicos continuam seguindo a mesma lógica.

Domínio de uma função hiperbólica

Olha primeiro para aquelas expressões lá do senh e do cosh, e vamos tentar encontrar os domínios desses caras.

Esses dois caras só tem o nas exponenciais ali no numerador, então não existe nenhuma restrição quanto ao domínio!

Para as demais relações hiberbólicas, teremos divisões, aí precisamos de cuidado com os pontos onde o denominador é zero.

O senh(x) zera no ponto . Então, as funções que tem senh(x) no denominador têm esse domínio aqui:

Já o cosh(x) nunca zera! Pode tentar achar algum valor de que vai zerar a expressão com a soma dos exponenciais lá 😉

Então, saca os domínios das funções que tem cosh(x) no denominador:

Imagem de uma função hiperbólica

A imagem de uma função são os valores que assume para cada valor de .

Vamos olhar para as definições de novo e tentar desenvolver um raciocínio aqui. Começando pelo senh:

Se substituirmos aí, a função vai ficar igual a zero. Agora, quando vai crescendo pra infinito, aquela parcela também cresce pra infinito. Só que a outra parcela, , tende a zero.

Então, quando tende a infinito, a gente fica com:

A função cresce infinitamente e abrange todos os números positivos.

Mas e se decresce, rumo ao infinito negativo? Aí teremos o seguinte:

A função se torna cada vez mais negativa, e a imagem abrange todos os números negativos.

Tudo isso, só pra te dizer que a imagem de senh(x) é todos os reais!

Bora fazer o mesmo raciocínio para o cosh(x)?

Só que aqui vou ser mais direto.

O termo do numerador vai ser sempre positivo, independentemente de qual substituirmos ali. Então, quando tende tanto ao infinito positivo quanto ao negativo, o cosseno hiperbólico sempre vai ser positivo e tender ao infinito positivo.

Além disso, quando , . Esse é o menor valor possível da função. Então, sua imagem abrange só valores maiores do que 1.

Gráficos das funções hiperbólicas

Vamos juntar todos as análises que fizemos até aqui (domínio, imagem e pontos críticos) pra chegar nos seguintes gráficos:

Para o :

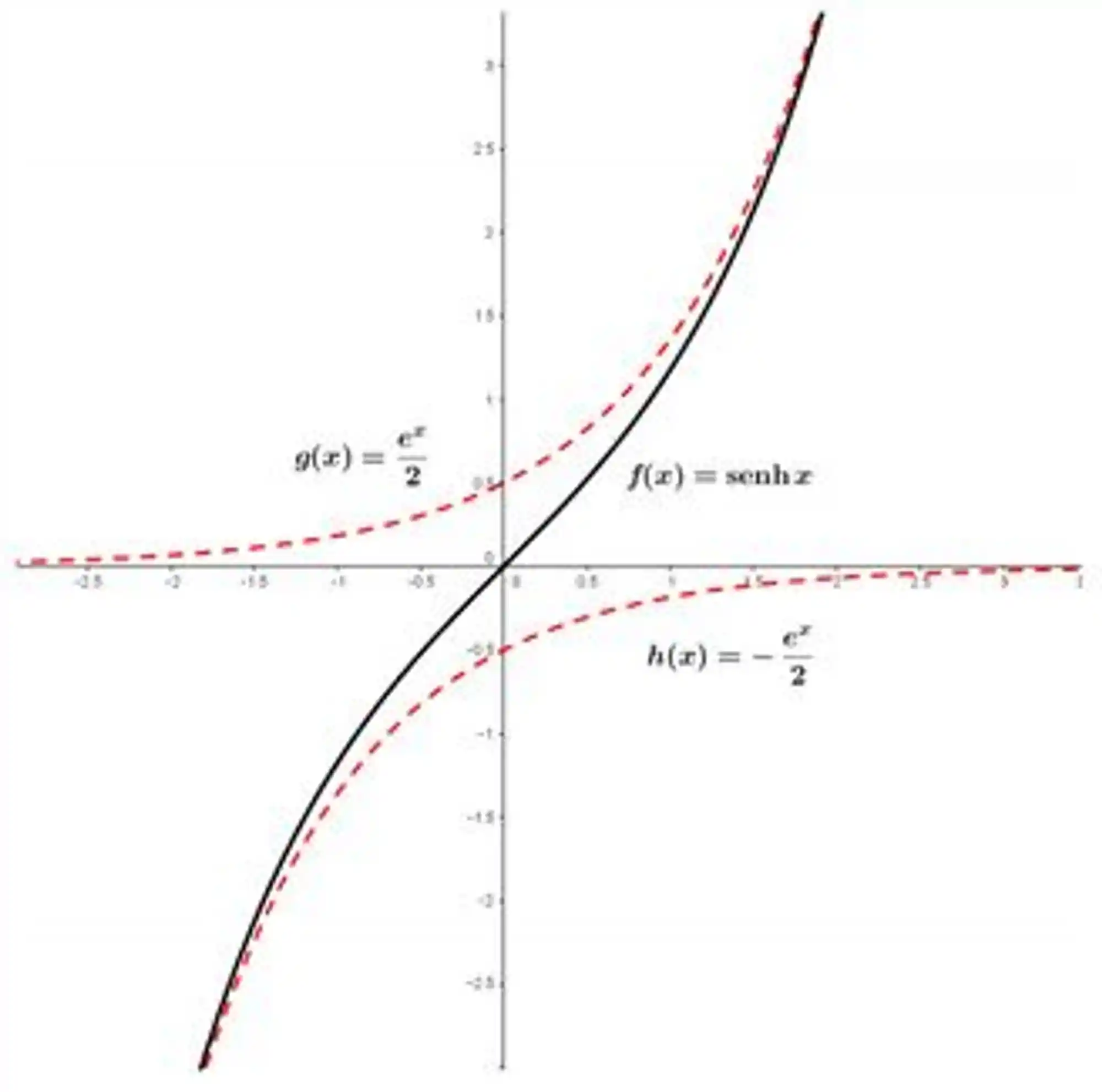
Gráfico do seno hiperbólico (senh).
Gráfico do seno hiperbólico (senh).

E para o :

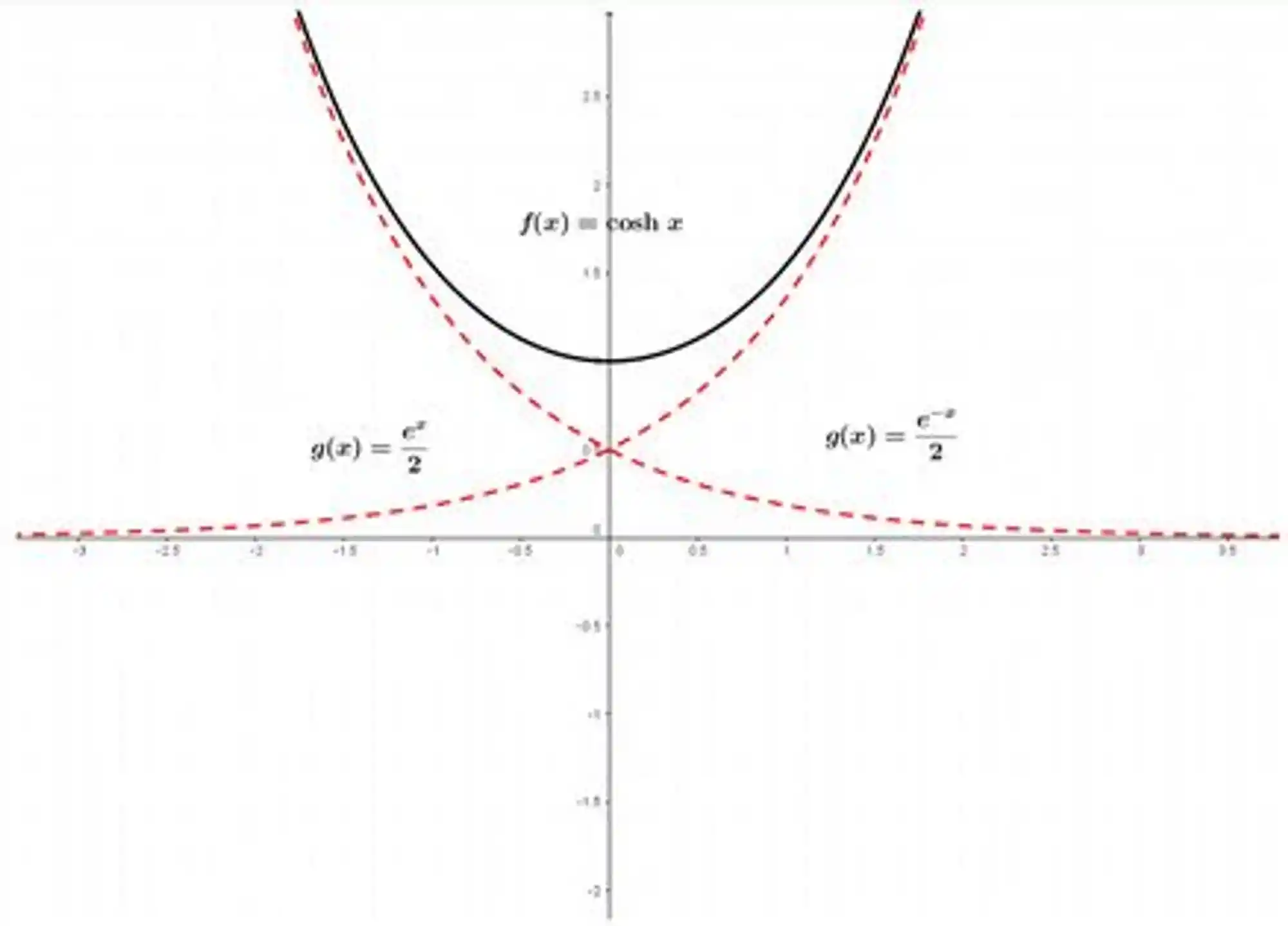
Gráfico do cosseno hiperbólico (cosh).
Gráfico do cosseno hiperbólico (cosh).

Derivadas de funções hiperbólicas

As derivadas das funções hiperbólicas são bem parecidas com as trigonométricas, só vão mudar alguns sinais aqui e ali.

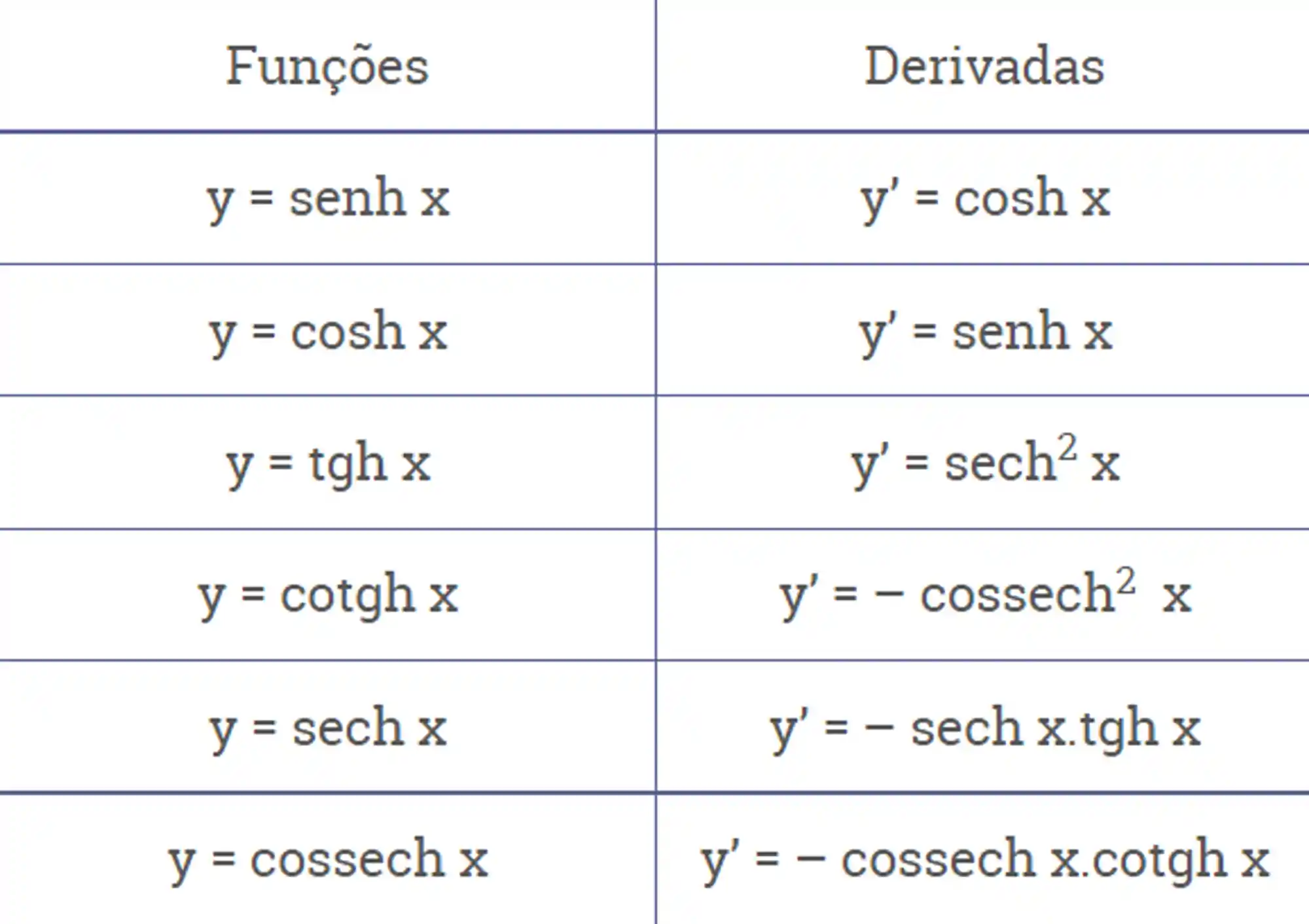
Tabela: Derivadas das funções hiperbólicas.
Tabela: Derivadas das funções hiperbólicas.

Então fica esperto pra não se confundir, viu?

Domínio de uma função hiperbólica

Imagem de uma função hiperbólica

Derivadas de funções hiperbólicas

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Dada a função

f x = sen h ⁡ x

Determine o valor de y para x = 0

Passo 1

Opa!!! Vamos lá!! Vamos primeiro observar como nós definimos o sen h ⁡ x lá na nossa teoria. Vimos que ele aparece assim...

sen h ⁡ x = e x - e - x 2

Certo?

Beleza!! Então vamos partir dessa definição!

Passo 2

Queremos o valor de y para x = 0 , então basta substituirmos esse valor na nossa função. Vai ficar assim ó..

senh ⁡ 0 = e 0 - e - 0 2

Isso vai ser igual a

senh ⁡ 0 = 1 - 1 2 = 0 2 = 0

Assim,

senh ⁡ 0 = 0

Show de bola?!

Resposta

0

Exercício Resolvido #2

Elaboração Própria

Reescreva a expressão em forma de exponenciais e simplifique o máximo que puder:

senh ⁡ x - cosh ⁡ x 2

Passo 1

Vamos lááá! Queremos simplificar a expressão

senh ⁡ x - cosh ⁡ x 2

Certo!? MAS PERA!! Primeiramente, não podemos confundir:

senh ⁡ x - cosh ⁡ x 2

Com

senh 2 ⁡ x - cosh 2 ⁡ x = - 1

Beleza?! Cuidado!

Como o problema quer o tudo em exponenciais, vamos aplicar a definição:

senh ⁡ x = e x - e - x 2 cosh ⁡ x = e x + e - x 2

Substituindo esses valores na expressão, temos

e x - e - x 2 - e x + e - x 2 2 = - e - x 2 = e - 2 x

senh ⁡ x - cosh ⁡ x 2 = e - 2 x

Show de bola?!

Resposta

senh ⁡ x - cosh ⁡ x 2 = e - 2 x

Exercício Resolvido #3

Elaboração Própria

Mostre que a função

f x =   s e n h ( x )

É uma função ímpar.

Passo 1

Vamos lááá!! Antes de qualquer coisa, vamos relembrar o que significa uma função ser ímpar?

Uma função será ímpar quando

f - x = - f x

Beleza?! Então vamos verificar se essa igualdade é satisfeita com a função f x =   s e n h ( x ) ?!

Passo 2

Podemos escrever a função senh ⁡ x da forma exponencial

senh ⁡ x = e x - e - x 2

Utilizaremos ela para verificar se a igualdade f - x = - f x

É verdadeira, beleza?!

Assim,

senh ⁡ - x = e - x - e + x 2

Da mesma forma,

- senh ⁡ x = - e x - e - x 2 = - e x + e - x 2

Ou seja,

senh ⁡ - x = - senh ⁡ x

Logo, a função s e n h x é ímpar!

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Elaboração Própria

Mostre que a função

f x =   c o s h ( x )

É uma função par.

Passo 1

Vamos lááá!! Antes de qualquer coisa, vamos relembrar o que significa uma função ser par?

Uma função será par quando

f - x = f x

Beleza?! Então vamos verificar se essa igualdade é satisfeita com a função f x =   c o s h ( x ) ?!

Passo 2

Podemos escrever a função senh ⁡ x da forma exponencial

cosh ⁡ x = e x + e - x 2

Utilizaremos ela para verificar se a igualdade c o s h - x = c o s h x

É verdadeira, beleza?!

Assim,

cosh ⁡ - x = e - x + e x 2

OPA! O a expressão que encontramos é exatamento a expressão de cosh ⁡ x = e x + e - x 2

Ou seja,

c o s h - x = c o s h x

Logo, a função cosh ⁡ x é par!

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Elaboração Própria

Mostre que a função

f x =   t g h ( x )

É uma função ímpar.

Passo 1

Vamos lááá!! Antes de qualquer coisa, vamos relembrar o que significa uma função ser ímpar?

Uma função será ímpar quando

f - x = - f x

Beleza?! Então vamos verificar se essa igualdade é satisfeita com a função f x =   t g h ( x ) ?!

Passo 2

Podemos escrever a função tg h ⁡ x da forma

tgh ⁡ x = s e n h x   cosh ⁡ x

Beleza?! Utilizaremos ela para verificar se a igualdade f - x = - f x

É verdadeira, beleza?!

Assim,

tgh ⁡ - x = s e n h - x   cosh ⁡ - x

Temos que a função s e n h x é uma função ímpar, então

senh ⁡ - x = - senh ⁡ x

Da mesma forma, a função cosh ⁡ x é par, então

c o s h - x = c o s h x

Assim,

tgh ⁡ - x = - s e n h x   cosh ⁡ x

Opa! A expressão que encontramos

- s e n h x   cosh ⁡ x =   - t g h x

Ou seja,

t g h - x = - t g h x

Logo, a função t g h x é ímpar!

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #6

Elaboração Própria

Dada a função

f x = cos h ⁡ x

Determine o valor de y para x=0

Passo 1

Vamos primeiro observar como nós definimos o cosh ⁡ x lá na nossa teoria. Vimos que ele aparece assim...

cosh ⁡ x = e x + e - x 2

Certo?

Beleza, se queremos o valor de y para x=0, basta substituirmos na nossa função... Vai ficar assim ó..

cosh ⁡ 0 = e 0 + e - 0 2

Isso vai ser igual a

cosh ⁡ 0 = 1 + 1 2 = 2 2 = 1

Tranquilinho, né?

Resposta

1

Exercício Resolvido #7

Elaboração Própria

Prove que

cosh 2 ⁡ x - senh 2 ⁡ x = 1

Passo 1

Para provarmos isso, vamos sair de um dos lados da igualdade e tentar chegar no outro... Por motivos lógicos, é muito mais fácil sairmos do lado esquerdo da igualdade e tentarmos chegar que isso é igual a 1. Vamos tentar?

Beleza, de início vamos trabalhar com as definições de cosh ⁡ x e   s e n h x . Sendo assim, teremos:

senh ⁡ x = e x - e - x 2   e       cosh ⁡ x = e x + e - x 2

cosh 2 ⁡ x - senh 2 ⁡ x = e x + e - x 2 2 - e x - e - x 2 2

Aplicando os produtos notáveis, teremos:

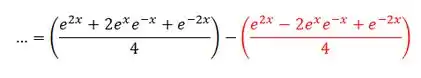
Reorganizando...

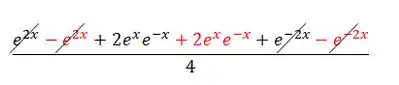
Lembrando que: 2 e x e - x = 2 e x - x = 2 e 0 = 2   .   1 = 2 , ficamos assim:

2 + 2 4 = 4 4 = 1

Como queríamos demonstrar.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

Elaboração Própria

Determine o valor de:

c o s s e c h ( ln ⁡ 2 )

Passo 1

Lembrando que a cossecante é o inverso do seno, podemos escrever o seguinte:

c o s s e c h ln ⁡ 2 = 1 s e n h ln ⁡ 2

Lembrando da definição de s e n h como

senh ⁡ x = e x - e - x 2

Podemos escrever:

c o s s e c h ln ⁡ 2 = 1 s e n h ln ⁡ 2 = 1 e ln ⁡ 2 - e - ln ⁡ 2 2 = 2 e ln ⁡ 2 - e - ln ⁡ 2

Agora, um pulo do gato importante:

e ln ⁡ 2 = 2                         e                   e - ln ⁡ 2 = 1 2

A gente sempre “corta” o e com o l n (Quando o log natural está no expoente)

Ah, mas por que ficou ½ ali?

Lembra que quando temos o sinal negativo no expoente a gente inverte?

O inverso de 2 é o 1/2, ok?

Show, agora só falta terminarmos essa parada...

Passo 2

Por fim, teremos o seguinte:

c o s s e c h ln ⁡ 2 = 2 e ln ⁡ 2 - e - ln ⁡ 2 = 2 2 - 1 2 = 2 3 2 = 4 3

Ou sejaaaa...

c o s s e c h ln ⁡ 2 = 4 3

Resposta

c o s s e c h ln ⁡ 2 = 4 3

Exercício Resolvido #9

Elaboração Própria

Determine o domínio e imagem de:

f x = senh ⁡ ln ⁡ x

Passo 1

Hummm. Antes de pensar no domínio, vamos tentar simplificar isso aí. Para tal, vamos aplicar a definição pelas exponenciais:

senh ⁡ x = e x - e - x 2 ⟹ senh ⁡ ln ⁡ x = e ln ⁡ x - e - ln ⁡ x 2 = e ln ⁡ x - 1 e ln ⁡ x 2

Podemos “cortar” o e com o l n :

… = x - 1 x 2 = 1 2 x 2 - 1 x

Passo 2

Veja só, conseguimos transformar uma sopa de hiperbólica com log em algo uma função racional.

O domínio dessa função excluirá os pontos onde o denominador zera. Isso ocorre em x = 0 , então ele não vai fazer parte do domínio, ficando:

D f x = R - 0

Passo 3

Vamos pensar na imagem agora. O que não é tão difícil. Veja que o numerador é uma parábola virada para cima com mínimo em - 1 , enquanto o denominador é x .

A parábola pode assumir valores negativos de - 1 até 0 e o numerador pode assumir qualquer valor positivo ou negativo, sendo que eles não trocam juntos de sinal. Dessa maneira, a imagem pode ser qualquer número real, e, portanto:

I m f x = R

Resposta

D f x = R - 0

I m f x = R

Exercício Resolvido #10

Elaboração Própria

Esboce o gráfico de:

f x = senh 2 ⁡ x + cosh 2 ⁡ x - 1 2

Passo 1

Não confunda essa expressão com identidade fundamental trigonométrica, lembre-se que:

senh 2 ⁡ x + cosh 2 ⁡ x ≠ 1

Mas sim:

cosh 2 ⁡ x - senh 2 ⁡ x = 1

Vamos então tentar usar essa identidade para simplificar f x e então esboçá-lo. Para tal, vamos tentar escrever a expressão de maneira que a identidade fundamental apareça.

Se somarmos e subtrairmos se nh 2 ⁡ x dentro da raiz estaremos somando zero e, portanto, não alterando nada, certo? Então vamos fazer isso:

f x = senh 2 ⁡ x + cosh 2 ⁡ x - 1 + senh 2 ⁡ x - senh 2 ⁡ x 2

Agora vamos reorganizar para aparecer a identidade:

f x = cosh 2 ⁡ x - senh 2 ⁡ x - 1 + senh 2 ⁡ x + senh 2 ⁡ x 2

Olha ela lá! Vamos substituir:

f x = 1 - 1 + 2 senh 2 ⁡ x 2 = senh ⁡ x

Passo 2

Agora ficou tranquilo, né? Já vimos esse gráfico na teoria. A diferença é que, por aparecer o módulo, a parte positiva estará refletida para cima:

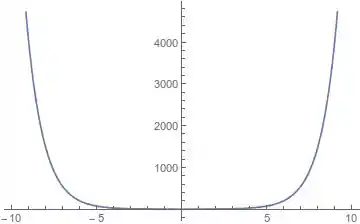
Resposta

Exercícios de Livros Relacionados

Prove que a função seno hiperbólico é contínua e crescente em todo o seu domínio.
Prove que a função cosseno hiperbólico é contínua em todo o seu domínio, mas não é monótona. Ache os intervalos nos quais a função é crescente e onde é decrescente.
Prove que a catenária é côncava para cima em todo ponto.OBS: Equação da catenária y = a cosh ⁡ x a Pra um a0
Uma partícula move-se ao longo de uma linha reta, de acordo com a equação de movimento s = e - c t 2 A senh ⁡ t + B cosh ⁡ t Onde sc m é a distância orientada da partícula até a origem em ts . Se vc m
Dado x = sen - 1 ⁡ 3 5 e y = cos - 1 ⁡ - 4 5 , ache o valor exato de cada uma das seguintes funções: a cos ⁡ x ; b sen ⁡ y ; c tg ⁡ x ; d tg ⁡ y