Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Capacitores

Ver Teoria
Exercício 61234578910

Enunciado

No circuito da figura abaixo, seja i s = 50 e - 2 t   m A e v 1 0 = 50   V , v 2 0 = 20   V . Determine:

(a)     v 1 t e v 2 t

(b) a energia em cada capacitor em t = 0,5   s .

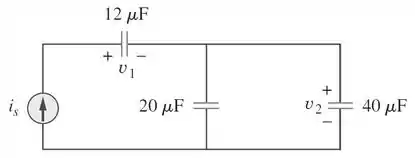
Passo 1

Vamos começar. A tensão em um capacitor tem a seguinte relação:

v t = 1 C ∫ - ∞ t i t d t + v ( t 0 )

Logo, para a tensão v 1 , temos:

v 1 ( t ) = 1 12 × 10 - 6 ∫ 0 t 50 e - 2 t × 10 - 3   d t + v 1 0  

v 1 ( t ) = 50 × 10 - 3 12 × 10 - 6 ∫ 0 t e - 2 t   d t + 50

v 1 ( t ) = 4166,67 ∫ 0 t e - 2 t   d t + 50

Passo 2

Vamos resolver a integral separadamente. Utilizando substituição simples, temos:

∫ 0 t e - 2 t   d t

u = - 2 t d u = - 2 d t

Substituindo:

- 1 2 ∫ e u d u   = - 1 2 e u

Voltando para t :

∫ 0 t e - 2 t   d t = - 1 2 e - 2 t t 0

∫ 0 t e - 2 t   d t = - 1 2 ( e - 2 t - 1 )

Passo 3

Substituindo o resultado da integral na equação de v 1 t :

v 1 t = 4166,67 - 1 2 e - 2 t - 1 + 50

v 1 t = - 2083,33 e - 2 t + 2133,33   V

Passo 4

Para calcular v 2 t , primeiro vamos calcular a capacitância equivalente entre os capacitores de 20 µ F e 40 µ F que estão em paralelo.

C e q = 20 + 40 = 60 µ F

Logo, temos o seguinte circuito:

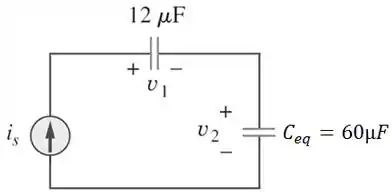
Passo 5

Então, vamos encontrar v 2 ( t ) .

v 2 t = 1 60 × 10 - 6 ∫ 0 t 50 e - 2 t × 10 - 3   d t + v 2 0

v 2 ( t ) = 50 × 10 - 3 60 × 10 - 6 ∫ 0 t e - 2 t   d t + 20

v 2 ( t ) = 833,33 ∫ 0 t e - 2 t   d t + 20

Já calculamos essa integral ali em cima. Substituindo o seu resultado:

v 2 t = 833,33 - 1 2 e - 2 t - 1 + 20

v 2 t = - 416,67 e - 2 t + 436,67   V

Passo 6

Agora, a gente precisa encontrar a energia de cada capacitor no instante t = 0,5   s . A relação da energia em um capacitor é a seguinte:

w = 1 2 C v 2

Passo 7

Primeiro, vamos calcular as tensões em t = 0,5   s .

Para v 1 :

v 1 0,5 = - 2083,33 e - 2 0,5 + 2133,33

v 1 0,5 = - 766,41 + 2133,33

v 1 0,5 = 1366,92   V

Para v 2 :

v 2 0,5 = - 416,67 e - 2 ( 0,5 ) + 436,67  

v 2 0,5 = - 153,28 + 436,67

v 2 0,5 = 283,39   V  

Passo 8

Vamos dar uma olhada no circuito.

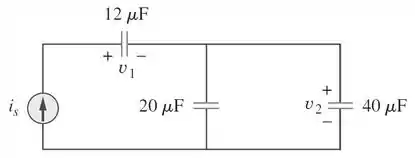
No capacitor de 12 µ F está sendo aplicada a tensão v 1 . Logo, a energia nele em t = 0,5   s , será:

w 12 µ = 1 2 12 × 10 - 6 1366,92 2

w 12 µ = 11,21   J

Como os capacitores de 20 µ F e 40 µ F estão ligados em paralelo, a mesma tensão v 2 está sendo aplicada nos dois capacitores. Logo:

w 20 µ = 1 2 20 × 10 - 6 283,39 2 = 0,803   J

w 40 µ = 1 2 40 × 10 - 6 283,39 2 = 1,606   J

Resposta

a )       v 1 t = - 2083,33 e - 2 t + 2133,33   V v 2 t = - 416,67 e - 2 t + 436,67   V        

b )   w 12 µ = 11,21   J w 20 µ = 0,803   J w 40 µ = 1,606   J

Exercícios de Livros Relacionados

O pulso de corrente de formato retangular mostrado na Figura P6.21 é aplicado a um capacitor de 0,1 mF. A tensão inicial no capacitor é uma queda de 15 V na direção de referência da corrente. Deduza a
A capacitância total de dois capacitores de 40m F em série associada em paralelo com um capacitor de 4m F é igual a:3,8 mF5 mF24 mF44 mF84 mF
Na figura abaixo, se i = cos ⁡ 4 r e v = sin ⁡ 4 r , o compomente é um:resistorcapacitorindutor
Para o circuito da figura abaixo, a fórmula para o divisor de tensão é: V 1 = L 1 + L 2 L 1 V s V 1 = L 1 + L 2 L 2 V s V 1 = L 2 L 1 + L 2 V s V 1 = L 1 L 1 + L 2 V s
Uma tensão CC de 10V é aplicada a um integrador com R = 50 k Ω , C = 100 μ F em t = 0 . Quanto tempo levará para o amplificador operacional saturar se as tensões de saturação forem + 12 V e - 12 V ? S