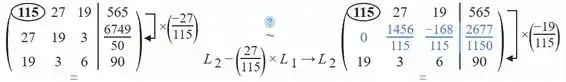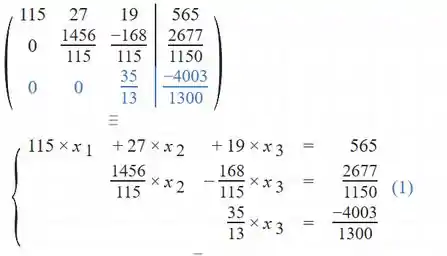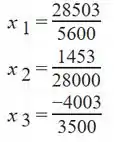Utilizando o método discreto, obtenha a reta que melhor se ajusta ao seguinte problema:
Passo 1
Temos que encontrar a reta que se ajusta bem aos pontos e resolve o sistema .
Considerando os dados:
Vamos montar uma daquelas famigeradas tabelinhas mágicas para resolver o sistema, contendo os seguintes somatórios: :
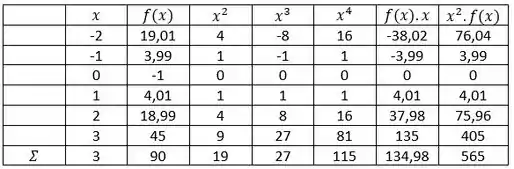
Com esses dados, conseguimos montar um sisteminha com os dados encontrados:
Passo 2
Solucionando o sistema por qualquer um dos métodos de resolução de sistemas lineares.
Link do programa: https://matrixcalc.org/pt/slu.html
Para facilitar a visualização, usaremos um programa que soluciona sistemas lineares pelo método de Gauss, que já vimos anteriormente e nosso objetivo aqui é entender o método dos mínimos quadrados!
Resposta
Exercícios de Livros Relacionados
13. Seja f ( x ) uma função real, de variável real, definida e contínua no intervalo [ 0,2 π ] e seja também n um número fixado.Ache os valores das constantes reais, a 0 , a 1 , … , a n , b 1 , b 2 ,
Um capacitor de capacitância CF a r a d , com carga inicial de q Coulomb está sendo descarregado através de um circuito elétrico que possui um resistor com resistência de RO h m s . Da teoria sabe-se