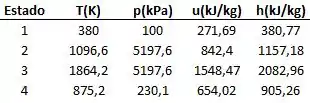
Considere um ciclo de ar-padrão Diesel. Os dados operacionais são fornecidos em seus estados principais no ciclo na tabela a seguir. Determine
a) A razão de corte.
b) O calor adicionado por unidade de massa.
c) O calor rejeitado por unidade de massa.
d) O trabalho líquido.
e) A eficiência térmica.
Passo 1
Vamos calcular a massa de ar pela equação dos gases perfeitos na forma:
A massa aparece aqui porque estamos utilizando o volume absoluto (em m³) ao invés do volume específico (em m³/kg) e também por estarmos utilizando a constante relativa ao ar, que já considera a massa molecular desta susbtância. Portanto, a massa pode ser calculada como:
Passo 2
Para achar o calor quente (adição de calor) e o calor frio (rejeição) vamos utiliazar as equações para troca de calor em isobáricas (adição) e isovolumétricas (rejeição), isso para o caso do Diesel.
Repare que utilizamos maiúsculo quando a massa entra na equação, pois resultará na quantidade de calor de fato (ao invés da quantidade de calor pela massa).
Então vamos calcular as temperaturas em 2 e em 3 para substituir na fórmula. Como o processo 1 – 2 é uma isentrópica então
Da mesma forma para o processo 3 – 4
A relação pode ser obtida a partir do processo 3 – 2 (isobárica) e vamos ter:
Repara que essa relação dos volumes é igual à razão de corte
E lembrando que o fator de compressão é dado por
E que , vamos ter
Então a relação entre e fica da forma
Voltando na fórmula
Passo 3
Agora que temos as temperaturas fica facinho facinho achar os calores:
Passo 4
E o trabalho líquido será dado por
E a eficiência