Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 1
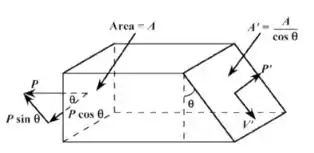
Usando os princípios da mecânica dos materiais (isto é, equações de equilíbrio mecânico aplicadas a um diagrama de corpo livre), derivar as Equações 6.4a e 6.4b.
Passo 1
Definimos como tensão:
Definimos como tensão de cisalhamento:
Considerando as equações de equilíbrios temos o diagrama de corpo livre a seguir:
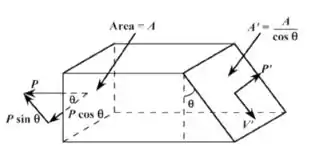
Considerando uma equação de equilibro temos que:
∑ Fx=0
Assim temos:
Agora substituindo na formula da tensão temos
Como vimos que σ= P / A podemos substituir na equação ali de cima e teremos essa equação:
Passo 2
Considerando o equilíbrio estático na direção y, sabemos que é necessário que o somatório das forças sejam iguais a zero.
Agora escrevemos uma expressão para τ ' (tensão cisalhante):
Agora podemos substituir “V” e “A” com o segundo somatório citado acima:
Como sabemos que σ= P/A
Resposta
Decomposição do diagrama de corpo livre em função da equação:
e
