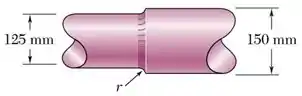
O eixo de seção variável da figura gira a . Sabendo que , determine a potência máxima que pode ser transmitida sem exceder a tensão de cisalhamento admissível de .
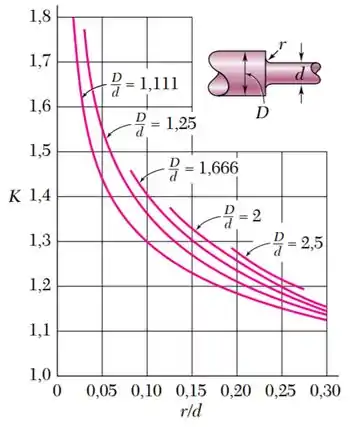
Utilize o gráfico abaixo para a determinação do coeficiente de concentração de tensão :
Passo 1
O que está acontecendo?
O eixo gira a uma frequência , transmitindo uma potência desconhecida , de forma a suportar um torque :
Ele possui um seção maior de diâmetro e uma seção menor de diâmetro , e, consequentemente, raio .
Além disso, existe um adoçamento de raio entre essas seções.
Nesse adoçamento, haverá uma concentrações de tensões na peça de tal forma que a tensão de cisalhamento máxima na peça vai ser:
Onde:
- é o coeficiente de concentração de tensão, que deve ser encontrado a partir do gráfico fornecido;
- & e são o raio e o momento polar de inércia da seção de diâmetro menor, uma vez que ela vai ter a razão maior, e, consequentemente, a tensão maior;
E o que é que o exercício quer?
Ele quer a potência máxima que pode ser transmitida pelo eixo de tal forma que a tensão cisalhante máxima na peça não ultrapasse a admissível :
Desenvolvendo a condição acima, é possível isolar e encontrar seu valor máximo.
Passo 2
Então vamos pegar a nossa condição de projeto:
E desenvolvê-la.
Primeiro, temos que, devido à concentração de tensões, .
Dessa forma, a nossa condição de projeto fica assim:
Em seguida, podemos aplicar a fórmula do torque em função da potência transmitida pelo eixo, deixando a condição assim:
E depois, podemos aplicar a fórmula do momento polar de inércia para uma seção transversal maciça e circular de raio , deixando a condição assim:
Arrumando tudo, temos que:
E, isolando a potência , encontramos que:
Agora, antes de podermos calcular essa expressão, temos que conhecer o coeficiente de concentração de tensão .
Então vamos atrás dele.
Passo 3
Para encontrar o coeficiente , precisamos recorrer ao seu gráfico:
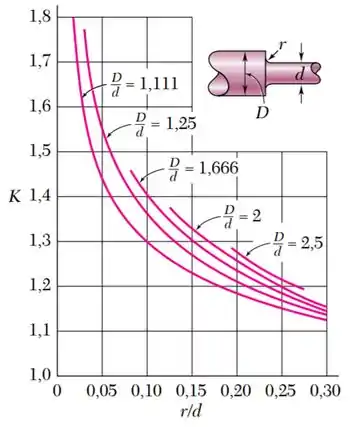
Do gráfico, vemos que é necessário calcular as razões e .
Calculando essas razões, encontramos que:
Ao tentar inserir essas razões no gráfico, percebemos que não existe uma curva .
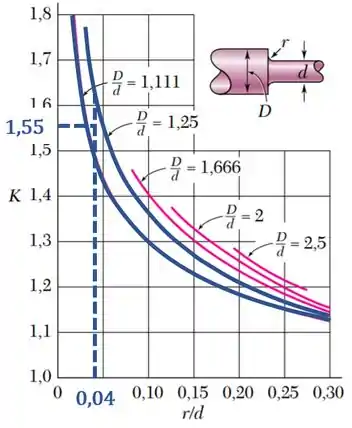
Então vamos usar as curvas mais próximas ( e ) e usar para um valor aproximado entre essas curvas.
Fazendo isso, encontramos que :
Passo 4
Agora, podemos voltar para a expressão que tínhamos:
E substituir os valores:
- ;
- ;
- ;
- & ,
Para encontrarmos que:
Calculando tudo isso, encontramos que:
Esse número é muito grande, então podemos reescrevê-lo em :
Agora pensa aí...
Newton () vezes metro é o mesmo que Joule ().
E Joule () por segundo () é o mesmo que Watt ().
Então:
Sendo assim, temos que a potência máxima que o eixo pode transmitir é: