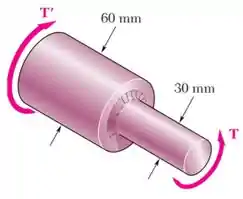
Sabendo que o eixo de seção variável mostrado na figura deve transmitir na velocidade de , determine o raio mínimo do adoçamento para que a tensão de cisalhamento admissível de não seja excedida.
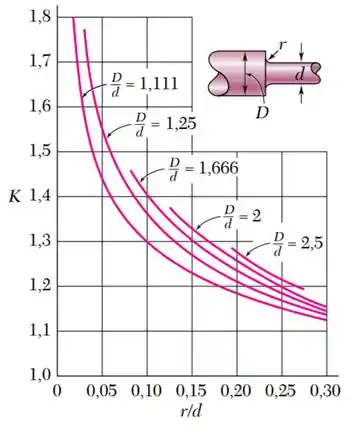
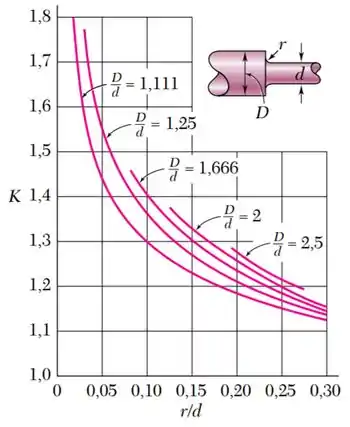
Utilize o gráfico abaixo para a determinação do coeficiente de concentração de tensão :
Passo 1
O que está acontecendo?
O eixo tem uma seção maior de diâmetro e uma seção menor de diâmetro , e, consequentemente, raio .
Entre essas seções, existe um adoçamento de raio .
Além disso, o eixo transmite uma potência a uma frequência , resistindo assim a um torque:
E o que é que o exercício quer?
Ele quer saber o raio mínimo de adoçamento para que a tensão de cisalhamento máxima no eixo não ultrapasse a admissível :
Sendo que, devido à concentração de tensões, sabemos que essa tensão máxima absoluta vai ser:
Onde:
- é o coeficiente de concentração de tensões, encontrado a partir de seu gráfico;
- & e são o raio e o momento polar de inércia da seção de diâmetro menor, uma vez que ela vai ter uma razão maior, e, consequentemente, uma tensão maior.
E como vamos resolver o exercício?
Vamos primeiro calcular qual é o coeficiente necessário para que a condição seja satisfeita.
Feito isso, vamos buscar no gráfico de qual é o valor de correspondente.
Passo 2
Então vamos pegar a nossa condição de projeto:
E desenvolvê-la, com o objetivo de encontrar qual o coeficiente necessário para satisfazê-la.
Primeiro, fazemos que , devido à concentração de tensões.
Fazendo isso, temos que:
Agora, podemos substituir a fórmula do momento polar de inércia para uma seção circular maciça de raio & a fórmula do torque :
Fazendo isso, temos que:
Arrumando tudo, isso fica assim:
E isolando , encontramos que:
Agora, substituindo:
- ;
- ;
- ;
- & ,
Encontramos que:
Como dessa forma, todas as unidades vão se cortar, isso fica assim:
Calculando tudo, isso dá aproximadamente:
Passo 3
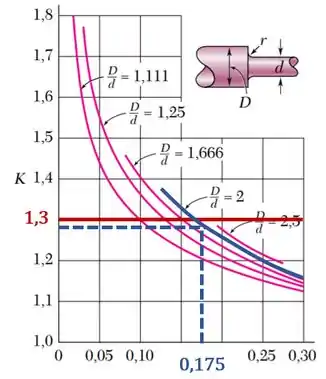
Agora, vamos observar o nosso gráfico para :
Primeiro, vemos que precisamos calcular a razão para identificarmos qual curva do gráfico devemos usar.
Fazendo isso, temos:
Destacando a curva e traçando uma linha em , vemos que uma estimativa para a menor razão que satisfaz a condição é :
Passo 4
Usando a estimativa do passo anterior, temos que:
Isolando , isso significa que:
Substituindo , encontramos que:
Calculando isso, encontramos nossa resposta final:
Observação: Como esse resultado final é baseado em aproximações, é de se esperar que diferentes alunos obtenham resultados diferentes.
Valores como ou também são boas aproximações!
Resposta
Por se tratar de uma aproximação, essa não é a única resposta possível, sendo respostas como ou também adequadas.