Uma barra uniforme de comprimento L e de massa desprezível e suspensa horizontalmente por uma dobradiça e uma corda, conforme figura ao lado.
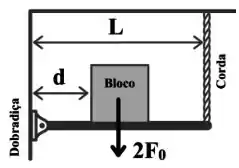
Um bloco de peso é colocado sobre a barra à uma distância d da dobradiça. Se a tensão da corda não pode exceder , qual o máximo valor de d e o módulo da força sobre a dobradiça nesta situação?
Passo 1
Para que esse sistema todo fique em equilíbrio estático temos que cumprir duas condições:
- Somatório de forças externas tem que ser zero
- Somatório dos torques externos em relação a qualquer ponto tem que ser zero também:
Onde .
Vamos considerar o nosso sistema somente a barra uniforme.Nesse caso, as forças atuantes são o peso do bloco (), a tensão na corda () e a força na dobradiça ().
Passo 2
Usando a primeira condição,
Como e o máximo valor de .
E repare que o peso aponta para baixo, enquanto as outras forças apontam para cima, então:
Passo 3
Vamos usar a segunda condição agora.
Para isso, precisamos escolher um ponto de referência para medir as distâncias. Eu escolhi a dobradiça, mas você podia escolher qualquer outro.
Como, em módulo, ,
Só não pode esquecer de tomar cuidado com os sinais! As forças que fazem o sistema girar no sentido horário devem ter sinais opostos às forças que fazem girar no sentido anti-horário.
Aqui, o peso do bloco gira no sentido horário em relação ao ponto de referência (eu o defini como positivo), logo a tensão na corda, que gira no sentido anti-horário tem que ter sinal inverso.