Um aquecedor de água apresenta área superficial igual a e está coberto com uma camada de isolante térmico. As temperaturas interna e externa da camada de isolante são respectivamente iguais a e . Sabendo que o material isolante apresenta condutividade térmica igual a , determine a espessura da camada isolante para que a transferência de calor do aquecedor seja igual a .
Passo 1
O exercício pede para calcular a espessura da camada isolante para que o aquecedor transfira uma determinada taxa de energia por calor à água .
Para isso, devemos recorrer à lei de Fourier e à simplificação que considera a distribuição de temperatura linear.
onde:
- é a espessura do isolante
- é a diferença de temperatura entre as superfícies interna e externa do isolante
- é a condutividade térmica
- é a área superficial onde ocorre a transferência de energia
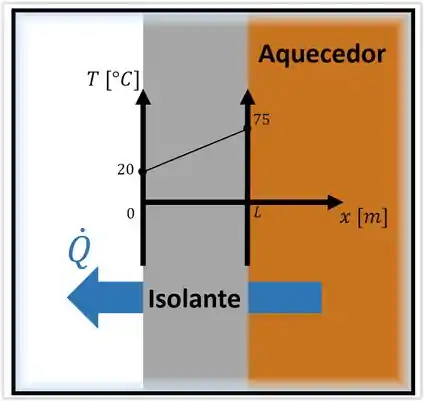
Substituindo a aproximação da linearidade na fórmula de condução, temos:
Para encontrar a espessura, temos que rearranjar a fórmula deixando a espessura sozinha de um lado e o resto das variáveis do outro.
Depois dessa etapa, veremos com mais facilidade que os quatro dados que devemos obter do enunciado para resolver o exercício são:
No fim, é só substituir os valores dados na fórmula reorganizada de condução para obter o resultado desejado.
Passo 2
Para rearranjar a fórmula simplificada de condução por calor, passamos para o lado esquerdo da equação e para o lado direito.
Passo 3
Essa útima etapa é só a substituição dos dados expostos no enunciado na equação que desenvolvemos.
Atenção! Como os valores substituídos estão de acordo com ao Sistema Internacional de Unidades, o resultado da conta resulta em um valor em metro!