Uma panela de aço (condutibilidade térmica igual a ) contém água líquida a 15°C. A espessura da panela é uniforme igual a e o diâmetro da panela é 0,2m. A panela é colocada sobre uma resistência elétrica que transfere ao fundo da panela. Admitindo que a temperatura da superfície interna da panela é uniforme e igual , determine a temperatura da superfície inferior externa da panela.

O exercício pede para calcular a temperatura da superfície inferior externa da panela . A função temperatura está presente dentro da derivada na lei de Fourier.

No entanto, recorrendo à simplificação, que considera a distribuição de temperatura como linear, conseguimos calcular a derivada e depois usá-la para calcular a temperatura desconhecida.

onde:

• é a espessura do isolante
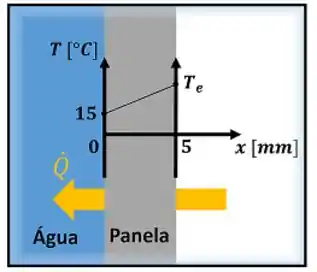
• é a temperatura da superfície externa da panela que desejamos calcular
• é a temperatura da superfície interna da panela
• é a condutibilidade térmica
• é a área superficial onde ocorre a transferência de energia

Segue abaixo a ordem das etapas que devemos cumprir para resolver a questão.

1. Reorganizar a lei de Fourier, explicitando a derivada da temperatura.
2. Substituir nessa fórmula os valores de condutibilidade térmica, da área superficial da base da panela e da taxa de energia fornecida à panela para obter o valor da derivda.
3. Reorganizar a relação, que associa a derivada e as temperaturas das superfícies, obtida através da simplificação para explicitar a temperatura da superfície externa.
4. Substituir os valores da espessura, da derivada da temperatura e da temperatura da superfície interna da panela pra calcular .

Para cumprir esses passos, é necessário listar o que foi dado pelo enunciado:

• Como o enunciado citou o diâmetro da panela, a forma de sua área, onde ocorre transferência de energia, é circular. Por isso: