Uma placa de compensado apresenta espessura igual . Sabendo que a diferença entre as temperaturas das superfícies expostas da placa é , determine a razão entre taxa de transferência de calor por condução da placa e a área de troca de energia.
Passo 1
O exercício pede para determinar a razão entre taxa de transferência de calor por condução da placa e a área de troca de energia. Mas o que a taxa de transferência de calor por condução significa? Para entender melhor o que esses termo significa, podemos ilustrar o problema.
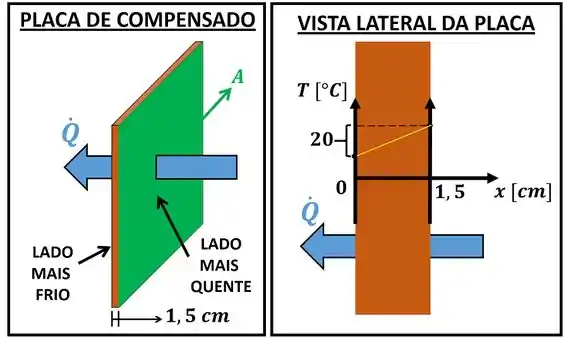
A taxa de transferência de calor é o nome comum, que os exercícios dão, para a derivada da energia que é transferida através da parede em relação ao tempo.
Para achar esse valor, temos que lembrar a fórmula de condução responsável pelo seu cálculo: a lei de Fourier.
Por essa equação, podemos ver que para encontrar a taxa de calor que atravessa a parede , precisamos primeiro achar o valor de três variáveis:
- A condutividade térmica
- A área onde a energia é trocada
- A derivada da temperatura em relação ao eixo
No entanto, a questão não pede o valor dessa taxa de transferência , mas sim a divisão de por . Ou seja, precisamos rearranjar a lei de Fourier, passando a área para o outro lado da equação, para calcular o que o problema quer. Faremos isso no próximo passo.
Passo 2
Reorganizando a lei de Fourier:
Agora vemos que, para obter o que se pede, não precisamos mais encontrar a área, porque o resultado da divisão só depende da derivada e da condutividade térmica.
Para chegar na resposta, temos que ler o enunciado com atenção, porque ele tem dois tipos de informação: as informações claras, que sabemos como usar, e os dados que ainda precisamos descobrir como usar na fórmula.
Vamos começar pelas informações mais claras:
- O enunciado diz que a condutividade térmica da placa de compensado vale .
- A função das outras duas informações ainda não está claramente definida. São elas:
- , a diferença de temperatura entre as duas superfície da placa
- , a espessura da placa
A primeira variável , fundamental para achar , já está determinada. Mas como calcular ?
Para essa tarefa, precisamos lembrar da simplificação mais comum desses exercícios:
- A temperatura varia linearmente com o eixo .
Passo 3
O eixo é a única direção, em que a temperatura da placa varia. No caso estudado, a diferença de temperatura entre as superfícies é a mesma. Ou seja, a temperatura só muda, conforme variamos a distância do ponto em relação a uma das superfícies.
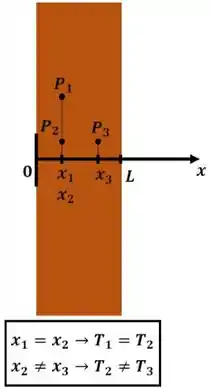
Vamos representar a variação linear da temperatura para facilitar o cálculo da sua derivada.
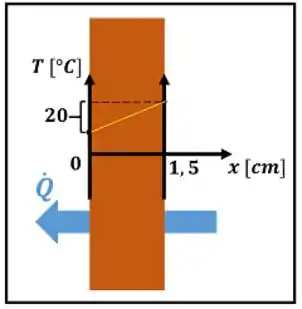
No fim, a derivada é igual à inclinação dessa reta!
Passo 4
Agora vamos calcular essa inclinação para determinar . Lembre-se de passar as unidades para o Sistema Internacional de Unidades (SI). Temos então que converter a espessura de milímetro para metro, antes de colocá-la na fórmula.
Passo 5
Essa etapa é só a substituição das duas variáveis na lei de Fourier rearranjada: