Uma parede plana composta consiste em uma camada isolante de de espessura e uma camada de tijolos de de espessura . A temperatura interna relativa ao isolante é . A temperatura externa dos tijolos é . Determine, em regime permanente, a temperatura na interface entre as duas camadas, em °C, e a taxa de transferência de calor através da parede, em por de área de superfície.
Passo 1
A primeira etapa para resolver esse problema é entender o que é uma parede composta. Ela é uma parede com duas camadas. Uma grudada na outra. As superfícies das paredes que estão juntinhas no meio têm a mesma temperatura , porque estão em contato! A primeira informação que o enunciado pede é justamente essa temperatura do meio!
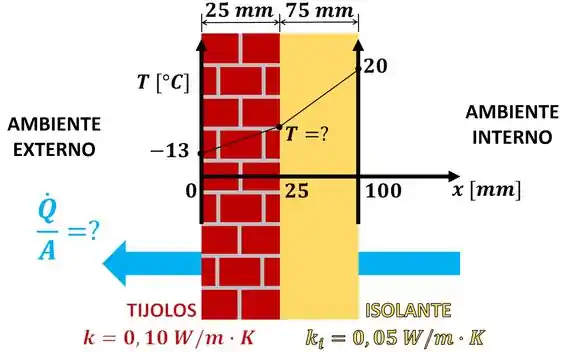
Observe que a figura acima já mostra as temperaturas variando linearmente com o eixo . Essa simplificação foi usada, porque o texto não fala como a temperatura varia! Então, com os dados informados, vamos escrever uma lei de Fourier para cada camada e ver o que temos, o que queremos e o que precisamos encontrar! Para a camada de tijolos, podemos escrever:
onde:
- é a última incógnita do problema
- é a última incógnita do problema
Para a camada de isolante podemos escrever:
onde:
Repare que a variável é a mesma pras duas equações. Por que isso contece se as duas camadas são diferentes? Respoderemos isso no próximo passo.
Passo 2
O enunciado diz que a transferência de calor ocorre em regime permanente! Mas o que isso significa? Significa que a taxa de calor que a camada isolante libera é igual à taxa de calor que a camada de tijolos recebe. Isso quer dizer que:
Ok, mas por que as áreas também são iguais? Por as duas camadas compõe a mesma parede. Ou seja:
Sabendo de tudo isso, conseguimos igualar as duas equações para criar uma fórmula de cálculo da temperatura do meio .
Rearranjando a posição dessas variáveis, achamos:
Com esse valor em mão, usamos a fórmula abaixo para descobrir quanto vale a outra incógnita.
Pronto, agora vamos para o próximo passo para fazer as contas.
Passo 3
Primeiro, vamos calcular quanto vale a temperatura das superfícies internas da parede .
Agora a próxima ingógnita pode ser calculada.