As temperaturas das superfícies interna e externa de uma janela de vidro x de de espessura no inverno são de e respectivamente. Se a condutividade térmica do vidro for igual a , determine a quantidade de calor perdido, em , através do vidro em um período de .
Passo 1
O exercício pede para determinar a quantidade de calor perdido através do vidro durante um período de . Mas o que isso quer dizer?

A quantidade de calor perdido é como chamam normalmente a quantidade de energia que atravessa o vidro. Essa quantidade é chamada de perdida, porque o fluxo de energia aponta da superfície interna da janela (maior temperatura) para sua superfície externa (menor temperatura). Isso significa que o cômodo protegido pela janela perde essa energia para o ambiente externo. O problema fica melhor explicado pela figura abaixo.
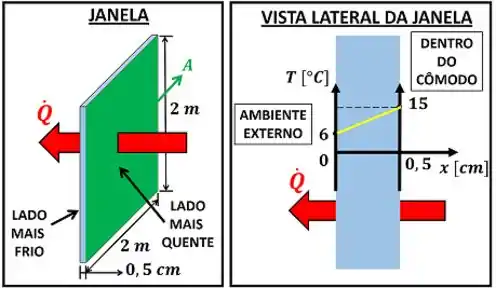
Mas então chegamos em um impasse! A fórmula que conhecemos de transferência de energia por condução (lei de Fourier), só calcula a derivada da energia que é transferida através do vidro em relação ao tempo. Falando de outra forma: essa conta só me dá a quantidade de energia transferida por segundo, não a quantidade transferida em dez horas.

Mas fique calmo que resolveremos esse dificuldade no próximo passo!
Passo 2
Pra resolver esse problema, precisamos perceber que o enunciado não cita nenhuma mudança nas condições de transmissão de energia. Ou seja, essa quantidade permanece constante com o tempo.

Então para fazer a conta, é só achar a energia transferida a cada segundo pela lei de Fourier e multiplicar esse valor pela quantidade de segundos que o período mencionado tem (3600 segundos relativos às 10 horas).
Por essa equação, podemos ver que para encontrar a taxa de calor que atravessa a parede precisamos primeiro achar o valor de três variáveis:
- A condutividade térmica
- A área onde a energia é trocada
- A derivada da temperatura em relação ao eixo
Para fazer isso, a gente precisa obter dois tipos de informação presentes no texto da questão: as informações claras e as que estão escondidos e temos que descobrir por dedução. Esse será nosso próximo passo!
Passo 3
Vamos começar pelas informações mais claras:
- O enunciado diz que a condutividade térmica da janela de vidro vale
- O valor da área também pode ser calculado rapidamente, mas ele não é informado diretamente como o . O tamanho da superfície de troca é mostrado, quando o enunciado expõe as dimensões x do vidro. Ou seja:
- A função das outras três informações ainda não está claramente definida. São elas:
- , a temperatura da superfície interna do vidro
- , a temperatura da superfície externa do vidro
- , a espessura do vidro
As duas primeiras variáveis e , fundamentais para achar , já estão determinadas. Mas como calcular ?

Para essa tarefa, precisamos de dois dados que estão escondidos no enunciado:
- A direção do eixo
- Saber como a temperatura varia nesse eixo
Passo 4
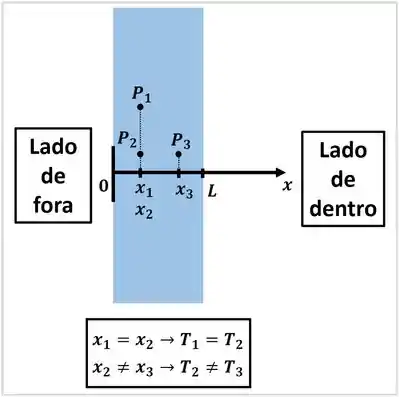
O eixo é a única direção, em que a temperatura do vidro varia. Mas como sabemos que essa simplificação de variação unidirecional da temperatura está sendo usada nesse caso?
Descobrimos isso, quando a questão diz que cada superfície do vidro tem apenas uma temperatura. Uma superfície está a e outra a .

Ou seja, a temperatura de um ponto não varia dentro de uma mesma superfície. Ela só muda, quando a distância entre o ponto considerado e uma das superfície se altera.
Como essa distância só muda conforme caminhamos em uma direção perpendicular às superfícies, o eixo é uma reta perpendicular às superfícies.
Falta agora saber como a temperatura varia ao longo da direção . A única pista do enunciado são as duas temperaturas que ele fornece.
A única função, que pode ser totalmente definida com dois pontos, é uma reta. Por isso, deduzimos que a questão está considerando uma distribuição linear para a temperatura.
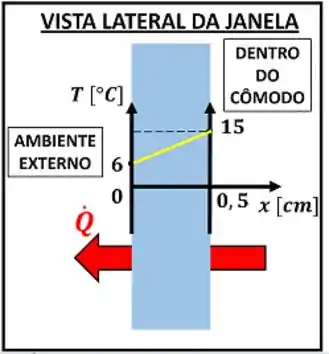
No fim, a derivada é igual à inclinação dessa reta!
Passo 5
Agora vamos calcular essa inclinação para determinar . Lembre-se de passar as unidades para o Sistema Internacional de Unidades (SI). Temos então que converter a espessura de centímetro para metro, antes de colocá-la na fórmula.
Passo 6
Essa etapa é só a substituição das três variáveis na lei de Fourier:
Passo 7
Agora é só calcular a quantidade total de energia perdida através de uma regra de três. Se o cômodo perde a cada segundo, quanto de energia ele perde em ?
Antes de dar essa resposta, temos que lembrar de converter esse valor em joule para a unidade pedida: quilojoule.