Um condensador de grande porte (trocador de calor) de uma central de potência precisa transferir da água que escoa no ciclo de potência para a água bombeada do mar. Admita que a parede de aço que separa a água de circulação da água do mar apresente espessura de , que a condutividade térmica do aço seja igual a e que a diferença máxima de temperatura permitida entre os dois fluidos seja de . Determine a área mínima desse condensador, desprezando a transferência de calor por convecção.

Essa questão é o típico exercício nos informa vários detalhes desnecessários para tentar fazer a gente pensar que ele é mais complicado do que realmente é! O que é uma central de potência? Por que a água que escoa nela vai transferir tanta energia para a água do mar? Não importa! O único fato que realmente faz a diferença é saber que os dois trocam calor separados por uma parede de aço. Isso está ilustrado na figura abaixo.

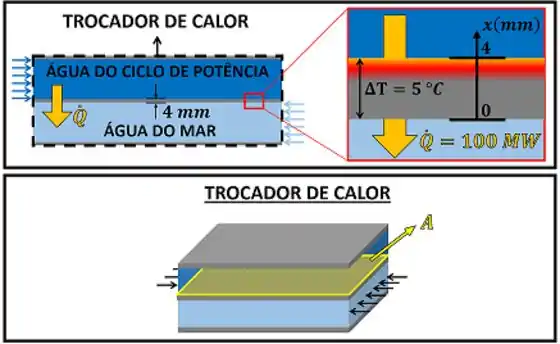
No fim das contas essa questão só quer saber qual é a área mínima de troca de calor . Podemos chegar nesse valor reorganizando a lei de Fourier.

onde:

Mas como podemos calcular a taxa de variação da temperatura em relação à posição ? Sempre que a questão não informar como a temperatura varia com o eixo , devemos assumir que essa distribuição é linear!

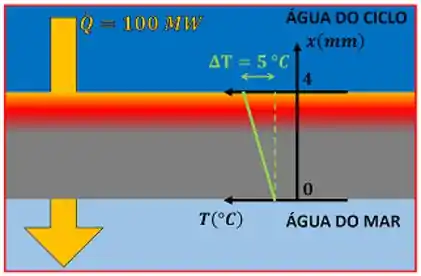
Por causa dessa simplificação, o cálculo de vira:

onde:

Pronto, temos todas as informações para iniciarmos os cálculos. Vamos fazer isso no próximo passo!