Três cascas esféricas concêntricas, de raios e respectivamente, são feitas de um material condutor perfeito de espessura desprezível. Em cada casca esférica está colocada a mesma quantidade de carga elétrica líquida igual a Q. As cascas esféricas estão em equilíbrio eletrostático. Não considere nenhuma outra carga na vizinhança das cascas esféricas ao responder às questões abaixo. Considere o centro do sistema de coordenadas coincidindo com o centro das cascas esféricas.
- Faça um desenho do sistema incluindo as cascas esféricas e os eixos de coordenadas.
- Calcule o vetor campo elétrico ao longo do eixo para as situações:
- ;
- ;
- ;
Passo 1
Fala galera, tudo bem? Vou ajudar você aqui!
Letra (a):
Vamos começar com um desenho. Vou reproduzir aqui um corte na vertical dessas cascas concêntricas. Cada casca deve ter carga líquida igual a , precisamos lembrar disso, ok?
Na casca mais interna temos a carga , na casca intermediária temos que na parte de dentro deve ter carga (para contrabalançar a carga da casca mais interna) e carga na parte externa da casca, para que no total tenha carga líquida igual a .
E na casca mais externa? Bom, na parte interior ela precisa ter carga , para contrabalançar a carga da parte de fora da carga do meio. E para ter carga líquida igual a , na parte externa da casca maior precisamos de uma carga .
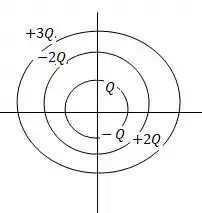
O desenho fica assim:
Passo 2
Letra (b):
Pela lei de Gauss o campo elétrico vai ser na direção para fora, e proporcional à carga que está contida dentro da superfície gaussiana. A forma geral desse campo é:
Na região não temos carga líquida dentro, logo ali o campo elétrico é zero:
Na região temos que apenas a carga da superfície mais interna contribui para o campo. Assim temos que nessa região e o campo ali é:
Já na região temos que tanto a casca mais interna, quanto a carga do meio contribuem, mas a mais externa não. Sendo assim a carga interna é e o campo é:
Por fim, na região , temos as três cascas contribuindo para o campo. A carga líquida interna é e o campo é:
Passo 3
Letra (c):
Densidade superficial é calculada assim:
A casca é esférica, então a área é . O raio é , pois é a casca mais externa. A carga total é a carga na superfície externa da casca mais externa que é . Agora é só substituir tudo:
Beleza?
Espero ter te ajudado!
Resposta