Três esferas condutoras isoladas têm inicialmente cargas , e . As esferas são todas do mesmo tamanho. Um fio condutor liga então as esferas e durante um certo tempo, até as mesmas atingirem um novo equilíbrio eletrostático. O fio entre e é então removido, e depois um outro fio passa a conectar as esferas e . Após um novo equilíbrio eletrostáticos ser atingido nas esferas e , esse segundo fio é também removido. Ao final do processo, as cargas em cada uma das esferas condutoras isoladas é:
(a) , e .
(b) , e .
(c) , e .
(d) , e .
(e) , e .
Passo 1
Vamos, inicialmente, olhar para a figurinha abaixo. Ela nos mostra as três esferas carregadas com as cargas , e dadas no início da questão.
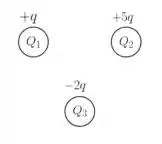
Passo 2
O próximo passo é conectar as esferas e até o equilíbrio eletrostático. Bem, o equilíbrio se dá quando as cargas se igualam, ou seja:
Sabemos também que a carga total deve se manter, ou seja,
Juntando as duas equações acima, chegamos em: , como é mostrado na figura abaixo.
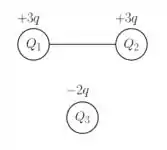
Passo 3
Por fim, retiramos o fio conectando as esferas e e conectamos as esferas e até um novo equilíbrio eletrostático.
O raciocínio é o mesmo do Passo 2, concorda? Vamos lá:
- Equilíbrio eletrostático é quando ;
- A carga total se mantém: ; e
- Chegamos, portanto, no resultado
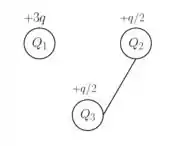
Resposta
As cargas em cada uma das esferas condutoras isoladas é
(d) , e .