Um conjunto cilindro-pistão fechado, contendo um vapor, perde calor a uma taxa constante de . Sabendo que a energia do vapor varia a uma taxa constante de e que esse processo de resfriamento é isobárico a , determine a taxa de variação do volume do vapor.
Passo 1
O exercício pede para a gente determinar a taxa de variação do volume do vapor . O primeiro passo para resolver essa questão é entender todas as informações do problema que o enunciado dá pra gente. Por isso, a figura abaixo mostra todos os dados que temos para calcular .
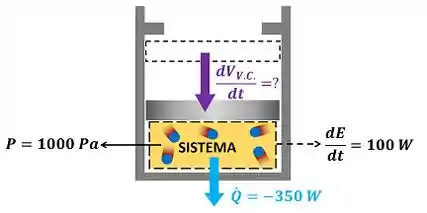
O da figura é a taxa de calor que sai do vapor. Como o vapor perde calor, essa taxa é negativa!
é a taxa de variação da energia do vapor. é a pressão do vapor durante o processo de resfriamento.
Esses são todos os dados que a questão nos informa. Agora, vamos determinar quais equações nós usamos para calcular .
Passo 2
Quando o vapor perde calor, seu volume diminui. Isso significa que o vapor comprime e recebe uma taxa trabalho de movimento de fronteira . Como esse trabalho é isobárico, a quantidade de energia por trabalho que o vapor recebe , quando a fronteira se movimenta pode ser calculado pela seguinte fórmula.
é a variação de volume do vapor. No entanto, nós não sabemos quando vale nem queremos calcular . Então como fazemos para transformar essa fórmula em uma equação que tenha as variáveis que precisamos calcular ( e )?

O primeiro passo para transformar a fórmula antiga é dividir todos os termos dessa equação pelo intervalo de tempo de duração processo .
O passo final é fazer o intervalo de tempo ficar cada vez menor. No limite, quando tende a zero, essas divisões viram derivadas! Ou seja, elas viram as taxas de variação em relação ao tempo!
Mas como podemos calcular com essa fórmula se não sabemos quanto vale ? Veremos isso no próximo passo!
Passo 3
Além disso, como o conjunto cilindro-pistão está fechado, não entra massa nele nem sai massa dele. Ou seja, o conjunto cilindro-pistão forma um sistema fechado. Então para calcular a potência do vapor, temos que usar a primeira lei para sistemas fechados.
Substituindo a fórmula de potência movimento de fronteira na equação acima, achamos a fórmula para calcular .
Olhando para a fórmula acima, nós vemos que temos informações sobre todas as variáveis que precisamos (, e ) para calcular . Então vamos começar a fazer as contas!
Passo 4
Atenção! O valor negativo de significa que o vapor comprimiu!