Uma panela com de água líquida a e a começa a ser aquecida a uma taxa constante de . Para aquecer a água mais rápido, uma pessoa derrama o total de de água quente na panela durante todo o seu aquecimento. Essa adição de água é constante e acrescenta de energia à panela a cada quilograma . No entanto, a panela perde o total de água com os respingos que saem dela constantemente. Esses respingos diminuem de energia da panela. Sabendo que esse aquecimento dura , determine a energia final da água que se encontra dentro da panela. Considere que a taxa de variação da energia da panela é constante. Despreze a variação de volume da água na panela. Use a tabela abaixo.
Passo 1
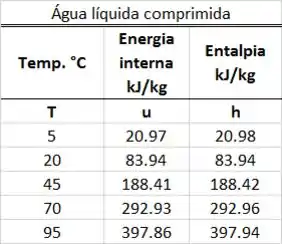
O exercício pede para a gente determinar a energia da água após ela passar por de aquecimento . O primeiro passo para resolver essa questão é entender todas as informações do problema que o enunciado dá pra gente. Por isso, a figura abaixo mostra todos os dados que temos para calcular .
O da figura é a taxa de calor que a água ganha. é a massa, é a pressão e é a temperatura da água antes de ser aquecida. é a energia por quilograma que sai da panela por causa dos respingos de água. é a energia por quilograma que entra na panela por causa da adição de água. é a duração do processo de aquecimento da água. é a quantidade total de água que entrou na panela e é a quantidade total de água que saiu da panela por causa dos respingos.

Passo 2
Como a panela está perdendo e ganhando massa de água, ela perde energia por conta dessa saída e dessa entrada de massa. Ou seja, a panela é um volume de controle. Por isso, temos que usar a primeira lei para volumes de controle.
Como a taxa de variação da energia da panela é constante que a derivada de uma reta, podemos calcular como a derivada de uma reta ! é a variação de energia da água na panela.
Por isso:
Mas é igual à energia que a água passou a ter depois de ser aquecida menos a energia que a água tinha antes de ser aquecida .
O primeiro passo para calcular é entender como encontrar o valor de todas as variáveis da primeira lei da termodinâmica acima! Para conseguir fazer isso, temos que entender primeiro o que cada termo significa! Esse será nosso próximo passo.
Passo 3
é a taxa de energia que entra no volume de controle por conta da entrada de massa no volume de controle. é a taxa de energia que sai do volume de controle por conta da saída de massa do volume de controle. é a taxa de trabalho realizado pela água dentro da panela.

Esses são todos os dados que a questão nos informa. Agora, vamos determinar como calcular cada termo da equação de !
Passo 4
Como a variação do volume da água na panela é desprezível, a água não realiza nem sofre trabalho. Por isso, a taxa de trabalho vale:
A taxa de energia que sai do volume de controle por conta da saída de massa é a vazão mássica de vapor que sai da panela através dos respingos multiplicada pela energia por quilograma de água que sai do tanque .
O problema é que ainda não temos o valor de massa que a panela perde a cada segundo. Conhecemos apenas o valor de massa que a panela perde no total. Como o enunciado diz que os respingos saem constantemente da panela, a taxa de saída de massa da panela é constante. Por isso é a massa total dividida pelo intervalo de tempo durante o qual a massa sai.
O mesmo raciocínio vale para calcular a vazão de entrada de água na panela a partir da quantidade total de água que a panela recebe . Como o enunciado diz que a adição de água na panela é constante, a taxa de entrada de massa na panela é constante. Por isso é a massa total dividida pelo intervalo de tempo durante o qual a massa entra.
Saber quanto vale é importante para calcular , porque faz parte da fórmula de .
No próximo passo vamos aprender a encontrar o valor da última variável que falta: .
Passo 5
A quantidade de energia que a água tinha antes dela ser aquecida é a energia interna específica dela multiplicada pela massa que ela tinha . A energia cinética e a energia potencial não aparecem nessa fórmula, porque a panela fica parada. Ou seja, ela não muda sua velocidade nem sua altitude.
pode ser encontrada pela tabela de propriedades do enunciado. O valor dela está na mesma linha da temperatura de e na mesma coluna da energia interna específica.
Depois de aprender isso tudo podemos iniciar as contas!
Passo 6
Vamos começar pelo cálculo de e .
Agora podemos calcular e .
Achamos o valor de através da tabela abaixo.
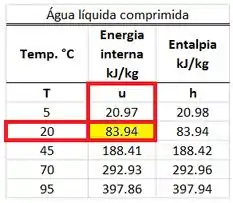
Com calculamos .
Substituindo na fórmula de :