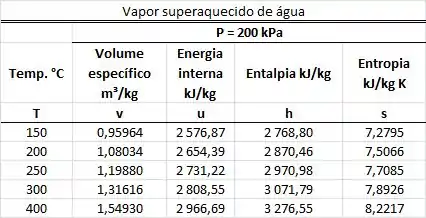
Um conjunto cilindro-pistão está vazando vapor superaquecido d’água por um furo com a uma velocidade média de . O vapor que sai está a e . Cada quilograma desse vapor diminui de energia do conjunto. O processo de vazamento dura e a taxa de variação da energia do vapor d’água presente no conjunto cilindro-pistão permanece constante durante esse intervalo de tempo. O pistão possui de diâmetro. Ele desce com uma velocidade de . Sabendo que o vapor do conjunto perde de calor durante esse processo e considerando que o processo de vazamento é isobárico, calcule a variação de energia do vapor dentro do conjunto do início ao fim do vazamento. Use a tabela termodinâmica abaixo.
Passo 1
O exercício pede para a gente determinar a variação da energia vapor superaquecido d’água do cilindro-pistão . O primeiro passo para resolver essa questão é entender todas as informações do problema que o enunciado dá pra gente. Por isso, a figura abaixo mostra todos os dados que temos para calcular .
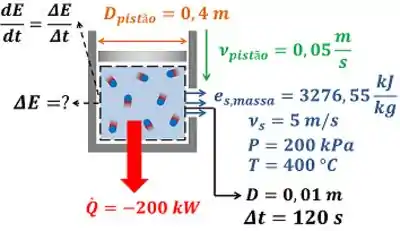
O da figura é a taxa de calor que o vapor d’água perde. é a pressão e é a temperatura do vapor que sai do cilindro-pistão. é a energia por quilograma que sai do cilindro-pistão por causa da saída de vapor. é a velocidade média do vapor saindo do cilindro-pistão. é a taxa de variação da energia do cilindro-pistão. é a duração do processo de vazamento do cilindro-pistão! é o diâmetro do furo por onde o vapor sai. é a velocidade com a qual o pistão se move. é o diâmetro do pistão.

Passo 2
Como o cilindro-pistão está perdendo massa vapor d’água, ele perde energia por conta dessa saída de massa. Ou seja, o cilindro-pistão é um volume de controle. Por isso, temos que usar a primeira lei para volumes de controle.
Como a taxa de variação da energia do cilindro-pistão é constante que a derivada de uma reta, podemos calcular como a derivada de uma reta !
Por isso:
O primeiro passo para calcular é entender como encontrar o valor de todas as variáveis da primeira lei da termodinâmica acima! Para conseguir fazer isso, temos que entender primeiro o que cada termo significa!

é a taxa de energia que entra no volume de controle por conta da entrada de massa no volume de controle. é a taxa de energia que sai do volume de controle por conta da saída de massa do volume de controle. é a taxa de trabalho realizado pelo vapor d’água de dentro do cilindro-pistão.
Esses são todos os dados que a questão nos informa. Agora, vamos determinar como calcular cada termo da equação de .
Passo 3
Quando o vapor perde calor e vaza, seu volume diminui. Isso significa que o vapor comprime e recebe uma taxa trabalho de movimento de fronteira . Como esse trabalho é isobárico, a quantidade de energia por trabalho que o vapor recebe , quando a fronteira se movimenta pode ser calculado pela seguinte fórmula.
é a variação de volume do vapor. No entanto, nós não sabemos quando vale nem . Então como fazemos para transformar essa fórmula em uma equação que tenha os dados informados pelo enunciado ( e ) e a taxa de trabalho precisamos achar ?

O primeiro passo para transformar a fórmula antiga é dividir todos os termos dessa equação pelo intervalo de tempo de duração processo .
O passo final é fazer o intervalo de tempo ficar cada vez menor. No limite, quando tende a zero, essas divisões viram derivadas! Ou seja, elas viram as taxas de variação em relação ao tempo!
pode ser calculado como a velocidade com a qual o pistão desce multiplicada pela área do pistão . Essa área é calculada a partir do diâmetro do pistão .
O sinal negativo é necessário, porque o volume de vapor diminui. Logo, a taxa de variação do volume é negativa.
No próximo passo, vamos aprender a calcular os termos que restam!
Passo 4
A taxa de energia que sai do volume de controle por conta da saída de massa é a vazão mássica de vapor que sai do cilindro-pistão multiplicada pela energia por quilograma de água que sai do cilindro-pistão .
pode ser calculada, multiplicando a vazão volumétrica de vapor pela massa específica da água! Só que a vazão volumétrica é a velocidade média da água saindo do cilindro-pistão multiplicada pela área do furo pelo qual o vapor sai .
A massa específica é o inverso do volume específico do vapor d’água.
Esse volume específico da água pode ser encontrado na tabela de vapor superaquecido. Seu valor está na mesma linha da temperatura de e na mesma coluna do volume específico.
Como não existe vapor entrando no volume de controle, vale:
Já sabemos como achar todas as variáveis da fórmula de . Então vamos começar a fazer as contas!
Passo 5
Primeiro devemos encontrar o da água na tabela.
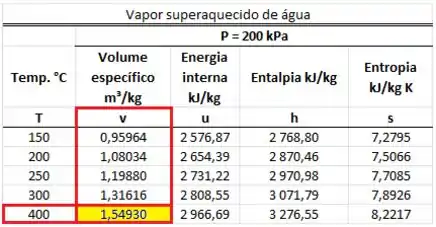
Com podemos encontrar .
Sabendo o valor de , conseguimos calcular a vazão mássica .
Todos os passos de cálculo realizados até agora serviram para achar .
A taxa de trabalho vale:
Enfim podemos calcular .