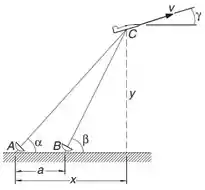
As estações de radar e , separadas pela distância , rastreiam o avião registrando os ângulos e em intervalos de um segundo. Se três leituras sucessivas forem

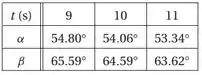
calcule a velocidade do avião e o ângulo de subida em . As coordenadas do avião são calculadas como

Vamos começar inserindo os dados fornecidos pelo enunciado. Em um novo script, entre com a distância e os dados da tabela:

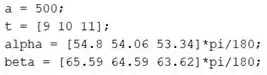
A primeira linha da tabela, que contém os instantes de tempo, é representada pelo vetor .

Os ângulos e da tabela são armazenados nos vetores e , respectivamente. Os ângulos são convertidos de graus para radianos, por meio da multiplicação por . Fazemos a conversão pois calcularemos as tangentes usando o comando do MATLAB, cuja entrada deve ser um ângulo em radianos.

Com os dados do enunciados implementados em nosso script, podemos calcular as coordenadas e do avião para cada um dos três instantes de tempo, usando as equações fornecidas pelo enunciado:

Note que, como e são vetores, o resultado de e também serão vetores, por isso, para realizarmos a multiplicação e a divisão nas equações das coordenadas do avião, devemos usar e , para fazer a operação entre cada elemento dos vetores.

A posição em e em do avião calculada a cada instante é armazenada nos vetores e , respectivamente. Esses vetores têm elementos, representando a posição nos instantes e .

Depois de calcularmos os vetores e , podemos determinar as componentes horizontal e vertical da velocidade do avião por meio de diferenciação numérica, calculando a derivada das posições e em relação ao tempo . Para encontrarmos e por diferenciação numérica, temos que gerar três vetores, um representando , outro representando e outro representando . Os vetores e teriam a diferença das posições e de instante de tempo a outro, respectivamente. Já o vetor teria a diferença entre um instante de tempo e outro.

Estes vetores são gerados por meio da função , que tem a estrutura:

Ela calcula vezes a diferença entre os elementos adjacentes do vetor e nos dá o resultado na forma do vetor . Como queremos que a diferença seja feita somente uma vez, não precisamos entrar com nenhum valor para na função , pois por padrão o MATLAB adota quando a entrada não é especificada.

Os três vetores são gerados por meio das seguintes linhas de código:

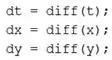
Na primeira linha, é criado o vetor , que contém as diferenças entre elementos adjacentes do vetor . Para criar o vetor , a funçao faz um elemento de menos o elemento à esquerda, começando a partir do segundo elemento de .

Na segunda e na terceira linha, é feita a mesma coisa, mas com os vetores e . A variação de é armazenada no vetor e a de , em .

Com os vetores , e criados, podemos calcular e por meio das linhas de código:

Com estes comandos, dividimos cada elemento do vetor e pelo elemento do vetor que esteja na mesma posição e os resultados são armazenados nos vetores e .

O vetor representa a derivada da posição do avião em relação ao tempo, indicando, portanto, a componente horizontal da velocidade do avião. Já o vetor representa a derivada da posição do avião em relação ao tempo, indicando a componente vertical da velocidade do avião.

O exercício pede para calcular a velocidade do avião e o ângulo de subida em . As componentes horizontal e vertical da velocidade em são os primeiros elementos dos vetores e , respectivamente. Vamos armazená-los nas variáveis e , para facilitar o cálculo da resposta do exercício:

Com e , podemos calcular a velocidade do avião, dada por:

Por isso, implemente em seu programa a linha de código:

A velocidade do avião é obtida ao executar o programa, dada pela variável , que é igual a:

O ângulo é dado pelo arcotangente de e em :

Para calcular o arcotangente, usaremos a função , que retorna o ângulo considerando os quatro quadrantes do círculo trigonométrico. tem como sintaxe:

Onde e são números reais, representando as coordenadas de um ponto no círculo trigonométrico, e é o ângulo em radianos. calcula o arcotangente da razão .

Por isso, inclua em seu programa a linha de código:

Com este comando, eu calculo o arcotangente de e converto o resultado de radianos para graus, por meio da multiplicação por . O ângulode subida do avião é armazenado em .

Rodando o programa, temos que é igual a: