Usando os dados da tabela a seguir, estime e
![]()
Passo 1
A questão nos pede para estimar a primeira e a segunda derivadas de em , a partir dos dados da tabela.
Para resolvermos o exercício, geraremos um gráfico com três curvas, uma representando , outra representando e outra representando , com indo de a . Faremos a estimativa de e a partir do gráfico, procurando o ponto nas curvas de e que tenha como coordenada .
Para gerarmos as curvas com função , precisamos calcular as derivadas de a partir da tabela, usando diferenciação numérica. Para isso, usaremos a função do MATLAB. Lembrando que ela tem a estrutura:
Ela calcula vezes a diferença entre os elementos adjacentes do vetor e nos dá o resultado na forma do vetor .
Para encontrarmos a derivada primeira, o vetor de entrada de será a função . Para a derivada segunda, o vetor será .
Passo 2
Primeiramente, crie um script novo no MATLAB e entre com os dados da tabela:
![]()
O vetor contém a primeira linha da tabela e o vetor , a segunda linha. Desta forma, o par de vetores e representa .
Depois de criarmos os vetores e , podemos determinar as derivadas primeira e segunda de . Vamos começar com a a derivada primeira. Para encontrarmos por diferenciação numérica, temos que gerar dois vetores, um representando e outro representando . O vetor teria a diferença de de um valor de a outro e o vetor teria a diferença entre um valor de e outro.
Estes vetores são gerados por meio da função , que tem a estrutura:
Ela calcula vezes a diferença entre os elementos adjacentes do vetor e nos dá o resultado na forma do vetor . Como queremos que a diferença seja feita somente uma vez neste exercício, tanto para calcular a derivada primeira quanto a segunda, não precisamos entrar com nenhum valor para na função , pois por padrão o MATLAB adota quando a entrada não é especificada.
Os dois vetores são gerados por meio das seguintes linhas de código:
![]()
Na primeira linha, é criado o vetor , que contém as diferenças entre elementos adjacentes do vetor . Para criar o vetor , a funçao faz um elemento de menos o elemento à esquerda, começando a partir do segundo elemento de .
Na segunda linha, é feita a mesma coisa, mas com o vetor . A variação de é armazenada no vetor .
Com os vetores e criados, podemos calcular por meio da linha de código:
![]()
Com este comando, dividimos cada elemento do vetor pelo elemento do vetor que esteja na mesma posição e o resultado é armazenado no vetor .
O vetor representa a derivada primeira de obtida por meio de diferenciação numérica. Com o vetor , podemos gerar o gráfico de .
Passo 3
Após determinarmos , podemos calcular , por meio de diferenciação numérica. Assim como fizemos para a primeira derivada no passo 2, para determinar , precisamos construir dois vetores, um representando e outro representando , e dividir um pelo outro.
Para isto, usamos a função de novo. No MATLAB, digite a linha de código:
![]()
Com este comando, aplicamos a função no vetor , que representa , e armazenamos o resultado no vetor . Calculando a diferença entre os elementos adjacentes de é como se estivéssemos calculando a derivada de , que é consequentemente .
é o nosso vetor representando . Para criar o vetor , vamos criar um vetor auxiliar chamado , com tamanho compatível ao vetor :
![]()
A linha de código acima diz que o vetor é um pedaço do vetor , começando do segundo elemento de e indo até o final de (indicando por ). Precisamos criá-lo pois o vetor tem um elemento a menos que o vetor e para calcular , precisamos que os vetores e tenham o mesmo comprimento.
Para criar o vetor , digite a linha de código:
![]()
O vetor contém a diferença entre os elementos adjacentes de e representa o vetor
Com os vetores e criados, podemos calcular por meio da linha de código:
![]()
Com este comando, dividimos cada elemento do vetor pelo elemento do vetor que esteja na mesma posição e o resultado é armazenado no vetor .
O vetor representa obtido por meio de diferenciação numérica. Com o vetor , podemos gerar o gráfico de .
Passo 4
Antes de gerar o gráfico de , e de , precisamos criar um vetor auxiliar para podermos plotar em função de .
Precisamos criar esse vetor auxiliar porque o vetor tem dois elementos a menos do que , já que ele na prática foi criado usando a função duas vezes seguidas. Vetores de tamanhos diferentes dão um erro na função .
Vamos chamar o vetor auxiliar de de e criá-lo com a linha de código:
![]()
Este comando diz que o vetor é um pedaço do vetor , começando do terceiro elemento de e indo até o final de .
Note que, para plotar em função de , podemos aproveitar o vetor do passo 3, já que tem o mesmo comprimento de.
Para plotar , e na mesma janela, digite as três linhas de código abaixo:

Na primeira linha, pedimos ao MATLAB para plotar em função de , em função de e em função de .
Na segunda linha, damos um nome ao eixo x do gráfico: chamamos ele de .
Na terceira linha, criamos uma legenda para o gráfico. A string é a legenda da curva gerada pelo primeiro par de vetores, e , da função . Já a string é a legenda da curva gerada pelo segundo par de vetores, e , da função . Finalmente, a string se refere ao terceito par de vetores da função , e .
Rode o programa para ver o gráfico:
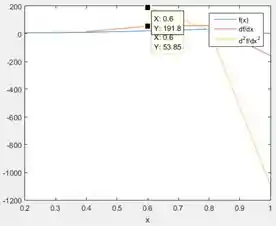
A curva azul representa , a curva vermelha é e a curva amarela, . Para estimar e , clique sobre as curvas vermelha e amarela, respectivamente, e procure o ponto com coordenada nas duas curvas (como no print acima). A coordenada desses pontos são a estimativa de e .
Resposta