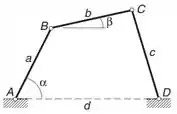
O mecanismo de quatro barras mostrado acima tem as dimensões , , e . Pode ser mostrado por geometria que a relação entre os ângulos e é
![]()
Para um dado valor de , podemos resolver esta equação transcendental para por algum método de determinação de raízes. Fazendo isso com temos os resultados
![]()
Se o elo gira com a velocidade angular constante de , use diferenciação numérica para tabular a velocidade angular do elo em relação a .
Passo 1
O enunciado nos dá uma tabela de em função de , o que nos permite calcular por meio de diferenciação numérica com o comando do MATLAB. Contudo, o exercício pede para encontrarmos para cada valor de .
Para encontrar , o enunciado nos informa que . Com esse dado, podemos obter a partir de e , usando o seguinte raciocínio:
Logo, para calcularmos , primeiramente calculamos usando o comando e, em seguida, multiplicamos o resultado por . Desta forma, temos para cada valor de .
Passo 2
Vamos começar calculando . Para isto, devemos entrar os valores da tabela do enunciado no MATLAB. Em um script novo, crie dois vetores, um para cada linha da tabela:
![]()
O vetor contém os valores da primeira linha da tabela, sendo convertidos de graus para radianos, por meio da multiplicação por . Já o vetor contém os valores da segunda linha da tabela, que já são dados em radianos.
Depois de criarmos os vetores e , podemos determinar por diferenciação numérica. Para isto, temos que gerar dois vetores, um representando e outro representando . O vetor teria a diferença de de um valor de a outro e o vetor teria a diferença entre um valor de e outro.
Estes vetores são gerados por meio da função , que tem a estrutura:
Ela calcula vezes a diferença entre os elementos adjacentes do vetor e nos dá o resultado na forma do vetor . Como queremos que a diferença seja feita somente uma vez, não precisamos entrar com nenhum valor para na função , pois por padrão o MATLAB adota quando a entrada não é especificada.
Os dois vetores são gerados por meio das seguintes linhas de código:
![]()
Na primeira linha, é criado o vetor , que contém as diferenças entre elementos adjacentes do vetor , logo, ele representa . Para criar o vetor , a funçao faz um elemento de menos o elemento à esquerda, começando a partir do segundo elemento de .
Na segunda linha, é feita a mesma coisa, mas com o vetor . A variação de é armazenada no vetor , que representa .
Passo 3
Com os vetores e criados, podemos calcular por meio da linha de código:
![]()
Com este comando, dividimos cada elemento do vetor pelo elemento do vetor que esteja na mesma posição e o resultado é armazenado no vetor .
O vetor representa obtida por meio de diferenciação numérica. A partir deste vetor, podemos calcular usando .
Passo 4
Para calcular , multiplicamos o vetor por . Por isso, vamos entrar com no MATLAB e em seguida realizar a multiplicação:
![]()
A variável represente e na linha seguinte, ela multiplica para obter para cada valor de , o que é armazenado em .
Os valores de representam para cada valor de a partir de , pois acabamos “perdendo” o primeiro elemento do vetor ao aplicar o comando .
O vetor é o resultado do exercício:
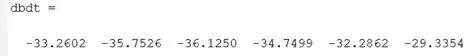
Resposta
![]()