A figura abaixo mostra um mecanismo biela-manivela:

A manivela AB tem comprimento = 90 mm e rotaciona a uma velocidade constante. A posição do pistão C varia de acordo com o ângulo segundo a equação:

Crie um programa que calcule a taxa de variação da posição do pistão em função de , para , usando diferenciação numérica. Ao final, plote as curvas de em função de e de em função de .

Primeiramente, crie um script novo no MATLAB e digite o código abaixo, para gerar um vetor contendo o intervalo de pedido no enunciado:

O comando acima cria um vetor chamado cujos elementos vão de 0° a 180°, com um passo de 5°, conforme exigido no enunciado. Os elementos de são convertidos de graus para radianos ao serem multiplicados por .

Em seguida, precisamos calcular para cada elemento do vetor . Para isso, usaremos um laço . Em seu script do MATLAB, digite as linhas de código:

Na primeira linha, eu entro com o comprimento da manivela AB, que é de 90 mm, armazenando-a em uma variável chamada .

Na segunda linha, crio um vetor que só tem zeros, com a função , que tem a seguinte estrutura:

A função cria uma matriz que só tem 0 em seus elementos. Ela tem como entrada o número de linhas da matriz de zeros que você quer criar, , e o número de colunas, .

O vetor criado na segunda linha tem uma linha e o mesmo número de colunas do vetor . Entramos com o número de colunas de usando a função , que nos dá a quantidade de elementos de .

Na terceira linha, começo com meu laço . Ele vai de 1 até a quantidade de elementos de , determinada pela função .

Na quarta linha, entro com a função que determina a posição do pistão em função de .

Finalmente, na última linha, encerro o laço .

Para encontrarmos por diferenciação numérica, temos que gerar dois vetores, um representando e outro representando . O vetor teria a diferença de posição do pistão de um ângulo a outro e o vetor teria a diferença entre um ângulo e outro.

Estes vetores são gerados por meio da função . Lembrando que ela tem a seguinte estrutura:

Ela calcula vezes a diferença entre os elementos adjacentes do vetor e nos dá o resultado na forma do vetor .

Os dois vetores são gerados por meio das seguintes linhas de código:

Na primeira linha, é criado o vetor , que contém as diferenças entre elementos adjacentes do vetor . Para criar o vetor , a funçao faz um elemento de menos o elemento à esquerda, começando a partir do segundo elemento de .

Na segunda linha, é feita a mesma coisa, mas com o vetor . A variação de é armazenada no vetor .

Note que não entramos nenhum valor para , porque queremos que a diferença seja feita uma vez. Quando não entramos com nenhum valor para na função , por o padrão o MATLAB adota .

Com os vetores e criados, podemos calcular por meio da linha de código:

Com este comando, dividimos cada elemento do vetor pelo elemento do vetor que esteja na mesma posição e o resultado é armazenado no vetor .

O vetor representa a derivada de em função de obtida por meio de diferenciação numérica. Em outras palavras, representa a taxa de variação da posição do pistão de acordo com o ângulo .

Com o vetor e , podemos gerar os gráficos pedidos no enunciado.

Antes de gerar o gráfico de e de em função de , precisamos criar um vetor auxiliar para podermos plotar a curva de . Esse vetor auxiliar é necessário por que o vetor tem um elemento a menos do que , o que levaria a um erro na função .

Vamos chamar o vetor auxiliar de e criá-lo da seguinte forma:

A linha de código acima diz que o vetor é um pedaço do vetor , começando do segundo elemento de e indo até o final de (indicando por ).

Já temos tudo o que precisamos para gerar os gráficos de e de . Vamos criar as curvas de ambos na mesma janela. Para isso, entre as três linhas de código abaixo:

Na primeira linha, pedimos ao MATLAB para plotar em função de e em função de .

Na segunda linha, damos um nome ao eixo x do gráfico: chamamos ele de e indicamos a unidade entre colchetes. Usei para sair o símbolo no gráfico.

Na terceira linha, criamos uma legenda para o gráfico. A string é a legenda da curva gerada pelo primeiro par de vetores, e , da função . Já a string é a legenda da curva gerada pelo segundo par de vetores, e , da função . Novamente, usei para sair o símbolo no gráfico.

Ao rodarmos o programa, é gerado o gráfico abaixo:

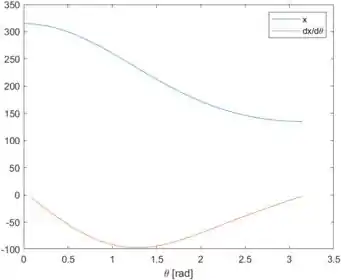
A curva azul representa a posição do pistão em função de .

A curva vermelha representa a taxa de variação da posição do pistão em função de , isto é, .