Exercícios Resolvidos de Deslocamento em Estruturas Isostáticas – Método das Tabelas
Ver TeoriaEnunciado
Calcule o deslocamento vertical do ponto C da viga dada abaixo usando o método das tabelas.
Use para todos os trechos da viga.
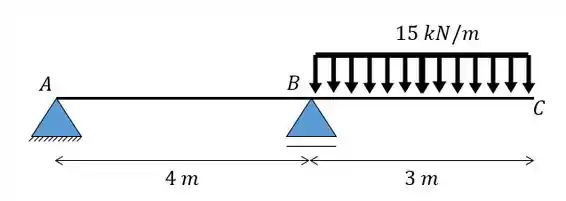
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Como a nossa equação é dada por:
Então podemos simplificar a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
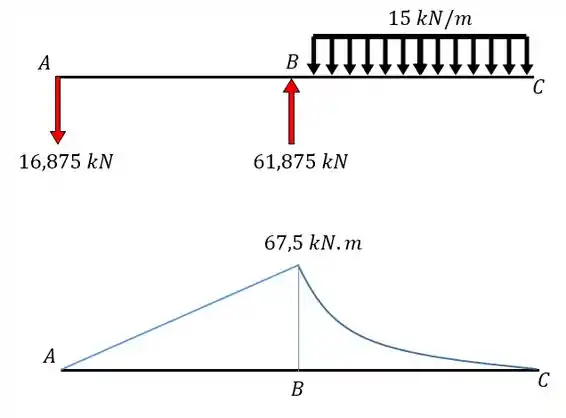
E perceba que existem duas funções distintas, uma para cada barra.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
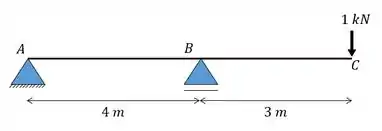
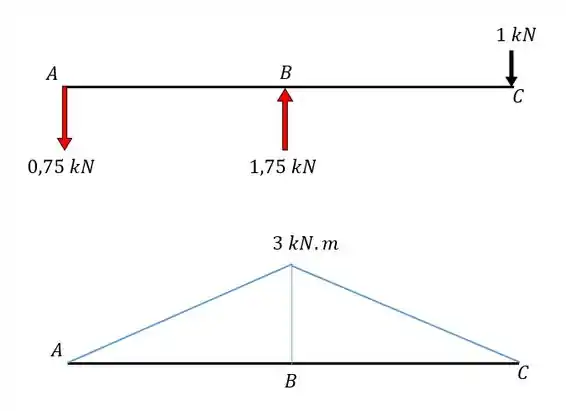
Passo 4
Passo 5
Passo 6
Determinação das combinações para cada uma das barras.
- Trecho AB
- Trecho BC
Primeiro temos as barras com os seus momentos.
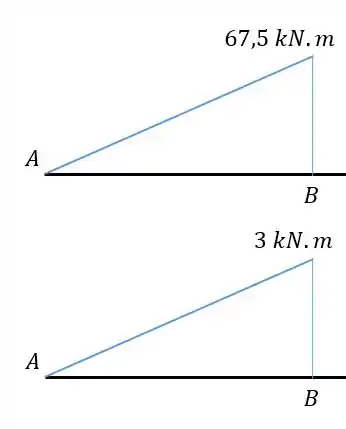
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:
E a fórmula será a combinação desses dois gráficos.
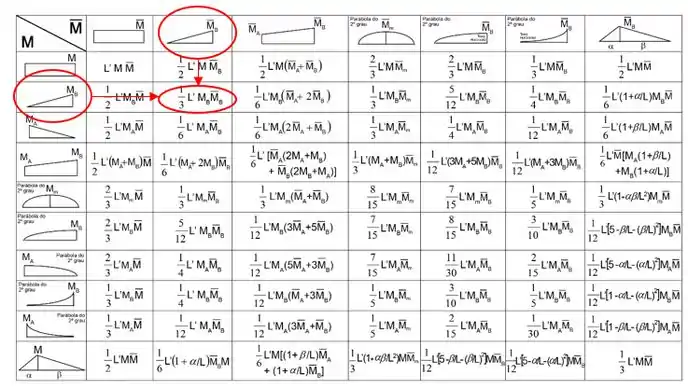
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra será igual a .
Substituindo na fórmula teremos que
Primeiro temos as barras com os seus momentos.
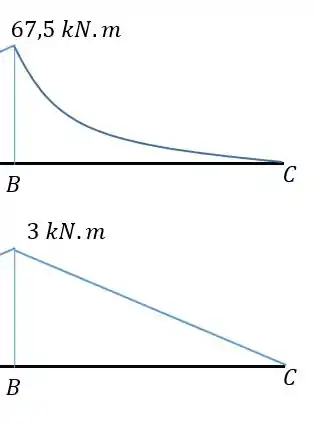
Usando a tabela temos: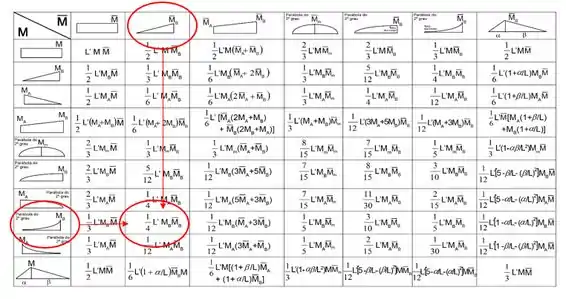 
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra será igual a .
Substituindo na fórmula teremos que
Passo 7
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que