Calcule o determinante da matriz abaixo.
Passo 1
Essa matriz parece muito grande né? Bom realmente ela é, mas podemos dar um jeito nisso. Repare que ela tem muitos zeros na e coluna, porém isso não é nada vantajoso para nós, pois precisamos de matrizes desse jeito:
Para podemos calcular o determinante por matrizes em blocos. Assim o que podemos fazer é trocar as duas últimas colunas com as duas primeiras:
Lembrando que como trocamos duas colunas o sinal do determinante não altera.
Passo 2
Agora sim podemos separar em blocos essa matriz:
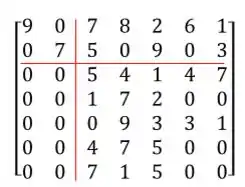
Tomando:
E assim:
Bom, chegamos de novo em uma matriz grande. Do jeito que ela está, não podemos dividir em blocos de zero do jeito que gostaríamos, o que podemos fazer é trocar a terceira linha com a segunda linha:
Passo 3
Agora vamos trocar a coluna com a e a com a :
E agora podemos separar a matriz em blocos:
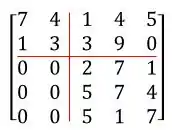
Assim seu determinante vai ficar:
Sendo:
E assim podemos finalmente calcular o determinante da nossa matriz :
Passo 4
Vamos começar calculando o determinante de :