Divida em blocos para calcular o determinante das matrizes abaixo (trocando linhas ou colunas de lugar se necessário).
Passo 1
Temos que dividir a matriz na forma:
De modo que no lugar do ou tenha pelo menos um bloco de zeros. Assim, podemos ver que na letra , podemos tomar E assim podemos aplicar a propriedade do determinante de matriz em blocos!
Como:
Podemos calcular o determinante da matriz original:
Passo 2
Bom, essa matriz já é um pouco mais difícil de calcular, pois não se enquadra nestes tipos: . O bloco de zeros está no lugar das matrizes e assim não dá pra aplicar a propriedade que queremos. Entretanto podemos trocar a coluna com a coluna e a coluna com a coluna , lembrando que o determinante muda de sinal cada vez que fazemos isso e como fizemos isso duas vezes o sinal volta a ser o original.
Agora sim temos uma matriz do tipo e podemos aplicar as propriedades! Mas antes, vamos separar quem são as matrizes :
Assim fica fácil de calcular o determinante da matriz original:
Passo 3
Dessa vez não temos um grupo quadradinho de zeros, mas lembre-se que não precisamos disso! Basta dividirmos um grupo de zeros com a matriz quadradas:
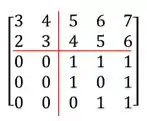
Assim, basta tomar:
Logo o determinante da nossa matriz é:
Resposta