Água a 20°C escoa por 10 m de tubo liso de 0,05 m de diâmetro a uma velocidade média de 8 m/s. Calcule a perda de carga em metros.
Passo 1
Opa! Para calcular a perda de carga , precisamos saber o fator de atrito , já que:
Substituindo os dados do enunciado (comprimento L, diâmetro D, velocidade média V)
Beleza, bora calcular esse fator de atrito!
Passo 2
O cálculo do fator de atrito depende se o escoamento é laminar ou turbulento. Para saber qual tipo de escoamento, o cálculo de Reynolds nos ajuda:
Como o fluido é a água e substituindo os dados do enunciado também
Para saber se é laminar ou turbulento, comparamos esse valor obtido com o valor de Reynolds crítico, que no caso do tubo é 2300.
Como Reynolds é maior que 2300, então o escoamento é turbulento!
Logo, o fator de atrito deve ser calculado pela rugosidade relativa e Reynolds aplicados no Diagrama de Moody.
Passo 3
Já conhecemos o Reynolds, mas não sabemos ainda a rugosidade relativa. Repara que o enunciado não informa o material do tubo, mas diz que ele é liso. Essa informação é suficiente para já utilizar o Diagrama de Reynolds
Utilizando a curva do tubo liso e no Diagrama de Moody,
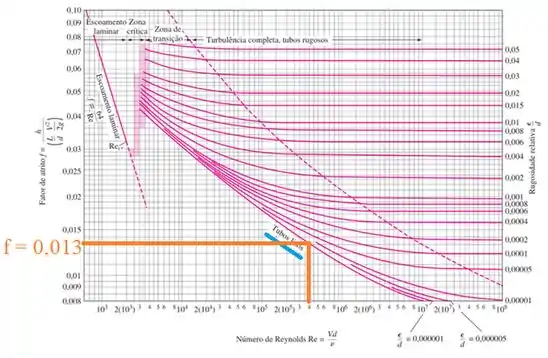
Encontramos que o fator de atrito é f = 0,013! :D
Passo 4
Voltando ao cálculo da perda de carga
Substituindo
Logo, a perda de carga é 8,5 m. Yay!