Os dados a seguir foram obtidos para o escoamento de de água a por um tubo com forte corrosão, de de diâmetro, que está inclinado para baixo a um ângulo de : , , , . Calcule (a) a rugosidade relativa do tubo e (b) a variação percentual na perda de carga se o tubo fosse liso e a vazão a mesma.
Passo 1
No enunciado ele já nos fornece o valor de algumas propriedades que aplicaremos na equação da energia:
Podemos dizer também que .
O esquema do problema é o seguinte:
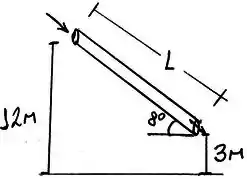
Passo 2
Na equação da energia, vamos calcular a perda de carga:
A massa específica da água é ,
Sabemos que
Desta expressão conhecemos tudo menos , e .
é facilmente cálculado pela geometria do problema:
Já é necessário dividir a vazão pela área transversal do tubo:
Dividimos a vazão por pois estava em e não em .
Colocando a expressão em função de :
Substituindo:
Passo 3
Calcularemos agora o número de Reynolds:
Viscosidade cinemática da água
Para , olhando no Diagrama de Moody a rugosidade relativa é aproximadamente igual a
Passo 4
Se o tubo fosse liso, para esse valor de Reynolds, o fator de atrito seria próximo a . Então a perda de carga seria:
Tomando a razão das duas perdas de carga:
Ou seja, a perda de carga no tubo liso seria menor comparado ao caso do tubo com forte corrosão.