Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Diagrama de Moody e fator de atrito

Ver Teoria
Exercício 61234578

Enunciado

Qual nível h deve ser mantido na Figura para fornecer uma vazão de 0,425   L / s pelo tubo de aço comercial de 13   m m de diâmetro?

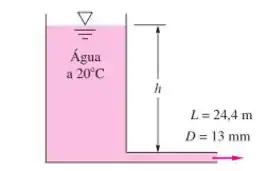
Passo 1

Como sempre galera, devemos ver o que precisamos calcular da equação da energia:

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Do desenho, podemos dizer que a pressão de entrada é a atmosférica, ou na escala manométrica.

p 1 = p 2 = 0

Podemos dizer também que,

z 1 = h

z 2 = 0

Supondo que o tanque de água tem uma superfície muito grande, logo:

V 1 = 0

O que nos resta de expressão:

h = V 2 ² 2 g + h p

Passo 2

Devemos calcular a velocidade de saída V 2 ,

V 2 = Q A

V 2 = 4 Q π D ²

Sabemos do enunciado que:

Q = 0,425 L s = 0,425 d m 3 s = 0,425 × 10 - 3   m ³ / s

D = 13   m m = 0,013   m

Substituindo,

V 2 = 4 0,425 × 10 - 3 π 0,013 ²

V 2 = 3,2   m / s

Passo 3

Agora para a perda de carga, calcularemos o Reynolds para termos o fator de perda de carga f :

R e d = ρ V D μ

Água a 20 ℃ : ρ = 1000   k g / m ³ e μ = 0,001   k g / ( m . s )

R e d = 1000 × 3,2 × 0,013 0,001

R e d = 41600

Temos um escoamento não laminar.

A rugosidade relativa é de,

ϵ D = 0,046 × 10 - 3 0,013 = 0,00354

O que nos leva a um fator de perda de carga no Diagrama de Moody:

f ≈ 0,028

Logo a perda de carga h p tem o seguinte valor,

h p = f L D V ² 2 g

h p = 0,028 24,4 0,013 3,2 ² 2 × 9,81

h p = 27,4   m

Passo 4

Subsituindo a perda de carga e a velocidade na expressão de h :

h = V 2 ² 2 g + h p

h = 3,2 ² 2 × 9,81 + 27,4

h = 27,9   m

Resposta

h = 27,9   m

Exercícios de Livros Relacionados

Petróleo está escoando de um grande tanque em uma colina para um petroleiro no cais. O compartimento de carga no navio está quase cheio e um operador inicia o processo de interrupção do escoamento. Um
Um tanque contendo 30 m3 de querosene deve ser esvaziado por gravidade usando uma mangueira de drenagem de diâmetro 15 mm, rugosidade 0,2 mm e comprimento 1 m. O topo do tanque está aberto para a atmo
Água a temperatura ambiente escoa à mesma vazão volumétrica, Q = 9,4 × 10 - 4m 3 / s , por dois tubos, um de seção circular e outro de seção anular. A área da seção transversal A dos dois tubos é idên
John Laufes (NACA Tech. Rep. 1174, 1954) forneceu dados de velocidade para escoamento de ar a 20°C em um tubo liso de 24,7 cm de diâmetro com R e ≈ 5 E 5 :A velocidade na linha de centro u L C era 30,
O sifão mostrado é fabricado de tubo de alumínio trefilado de 50 mm de diâmetro interno. O líquido é água a 15°C. Calcule a vazão volumétrica através do sifão. Estime a pressão mínima no interior do t