Depois de , as moedas de centavos de dólar passaram a ser fabricadas de modo que seus pesos tenham distribuição normal, com média de e um desvio-padrão de . Algumas máquinas de venda são planejadas para que você possa ajustar os pesos das moedas de centavos que serão aceitas. Se muitas moedas falsas são encontradas, você pode diminuir a amplitude dos pesos das moedas aceitáveis, com o efeito de que muitas moedas falsas serão rejeitadas junto com algumas poucas moedas legítimas.
a) Se você ajusta máquinas de venda para aceitar pesos entre e , que porcentagem de moedas de centavos legítimas é rejeitada?
b) Se você ajusta máquinas de venda para aceitarem todas as moedas legítimas, exceto aquelas com pesos nos superiores e nos inferiores, quais são os limites dos pesos daquelas que serão aceitas?
Passo 1
Ooi pessoal, como vocês estão?
Nessa questão temos um probleminha de distribuição normal. Basicamente, o peso das moedas de centavos de dólar seguem uma distribuição normal com:
Para burlar possíveis falsificações de moedas, máquinas de venda procuram restringir o intervalo de pesos que aceitarão como uma moeda legítima.
Assim, o item a) nos pede para calcular a porcentagem de moedas legítimas que é rejeitada, se limitarmos nossa máquina para aceitar pesos apenas entre e .
Tranquilo?!
Então, como trata-se de uma distribuição normal, podemos imaginar aquele gráfico de em forma de sino e tentar representar a nossa situação:
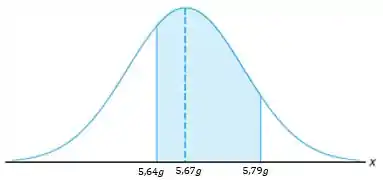
O intervalo de valores que será aceito pela máquina é justamente a região azul, mas toda região à esquerda e à direita dos extremos, representa moedas legítimas que serão rejeitadas.
Sendo assim, precisamos calcular justamente essas probabilidades. Ou seja:
Perfeito! Vamos então usar a distribuição normal para calcular cada uma dessas probabilidades.
Passo 2
Bom, vamos começar calculando .
Sabemos que essa distribuição normal possui:
Assim, temos:
A prova nos trouxe a tabela justamente para esse tipo de probabilidade (:
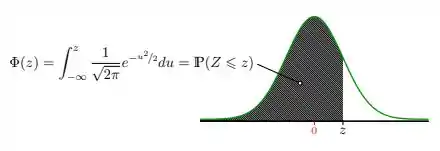
Sendo assim, vamos consultá-la para :
Perfeito!
Agora, vamos calcular .
Normalizando novamente, temos:
O problema agora é que a tabelinha dada só nos ajuda a calcular probabilidades do tipo , então podemos usar que:
Pela tabelinha, temos que:
Logo:
Excelente!
Como havíamos afirmado no passo :
Passo 3
Vamos para o item b).
Agora queremos aceitar todas as moedas que estão entre os 2,5% inferiores e os 2,5% superiores. Precisamos determinar quais os valores dos pesos da moeda correspondem a esses extremos.
Tranquilo? Vamo lá!

Começando pelos inferiores, concorda então que é equivalente a dizer:
Analisando a tabela, temos que:
Assim:
Logo:
Já para o limite superior, como também trata-se do top , a distribuição normal tem a propriedade de que esses limites devem afastar-se igualmente da média. Assim:
Logo:
Portanto, os limites são:
E é isso galera! Matamos mais uma questãozinha.
Espero que vocês tenham curtido a solução 😊
Resposta
a)
b)