Considere o seguinte conjunto de dados referente ao número de peças defeituosas produzidas por dia por uma máquina após um mês de operação:
![]()
Após traçar um histograma com estes dados utilizando-se oito classes, é possível afirmar que a sua distribuição de frequências é:
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Vamos lá! A questão nos deu um conjunto de dados numéricos onde cada número representa uma peça defeituosa fabricada num período de 1 mês.
A ideia principal dessa questão é construir um histograma de 8 classes com base nesse conjunto numérico e classificar sua distribuição de frequência como assimétrico à direita, assimétrico à esquerda, simétrico, bimodal ou trimodal.
O conjunto numérico foi dado como
![]()
Para facilitar nossa visualização dos passos a seguir, vamos escrever esse conjunto número em ordem crescente.
![]()
Com um objetivo da questão definida e os dados organizados podemos começar a pensar na resolução do problema.
Passo 2
Analisando o nosso conjunto vemos que nenhum número se repete, portanto, o nosso conjunto numérico não possui nenhuma moda, logo é classificado como amodal.
A partir dessa afirmação podemos descartar as opções d) e e) que dizem que o conjunto é classificado como bimodal e trimodal, respectivamente.
O próximo passo é construir um histograma de 8 classes pra isso vamos pegar a diferença do maior valor com o menor valor do nosso conjunto numérico e dividir por 8, formando assim, 8 classes no nosso histograma.
Com esse resultado vamos utilizar um espaço numérico entre 16 e 120 onde cada subespaço terá 16 números, por exemplo:
E assim sucessivamente até a classe 8.
Perceba que somamos o número inicial pois o número inicial conta como um número dentro da classe e cada classe deve ter 13 números.
Assim vamos ter:
Podemos fazer mais uma organização dos dados antes de elaborar o histograma.
Passo 3
Já definimos as classes, não vamos calcular a moda de cada número mais sim a moda de cada classe dessa forma cada classe vai se comportar como um número e quanto mais números dentro de uma classe se repetir no nosso conjunto numérico, maior será a moda da classe.

Construindo um histograma com as 8 classes temos:
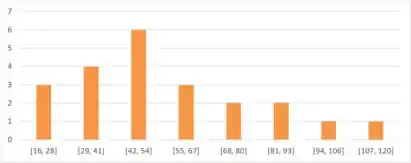
Classe 1 se repete 3 vezes, a Classe 2 se repete 4 vezes, a Classe 3 se repete 6 vezes, a Classe 4 se repete 3 vezes, as Classes 5 e 6 se repetem 2 vezes e as Classes 7 e 8 se repetem 1 vez.
Mas como classificamos este histograma?
A classificação entre assimétrico à direita, assimétrico à esquerda e simétrico, é dado pela regrinha
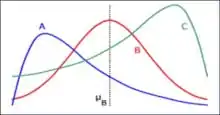
Se o gráfico do histograma se parecer com a curva A, onde a moda está à esquerda da mediana do gráfico, a classificação da frequência é dada como assimétrica positiva ou assimétrica à direita.
Se o gráfico do histograma de parecer com a curva B, onde a moda está no mesmo ponto da mediana, a classificação da frequência é dada como simétrica.
Por fim, se o gráfico do histograma se parecer com a curva C, onde a moda está à direita da mediana do gráfico, a classificação da frequência é dada como assimétrica negativa ou assimétrica à esquerda.
Passo 4
Analisando nosso histograma vemos que a curva se comporta como a curva A, já que a moda do histograma é a classe 3 que está à esquerda da mediana do gráfico.
Ou seja, nossa distribuição de frequências é classificada como assimétrica à direita ou assimétrica positiva.
Portanto a resposta correta é a letra A!

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
A) Assimétrica à direita.