Determine o campo vetorial gradiente .
Passo 1
Para determinarmos o campo vetorial, devemos tomar o gradiente da função , ou seja,
Lembrando que o gradiente de uma função é definido por um vetor, cujas as componentes são as derivadas parciais em cada direção, ou seja
Passo 2
Vamos tomar inicialmente a derivada de na direção .
E na direção temos
Desta forma escrevemos que
Passo 3
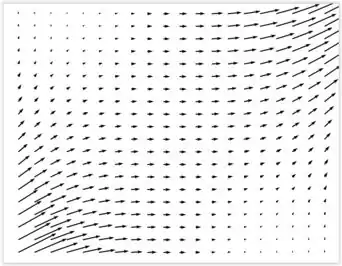
Uma representação do campo é dada pela figura a cima.