Transformada de Laplace em circuitos
Produzido por Alexandre NunesTeoria
Motivação
Nós vimos que é possível determinar a resposta , que pode ser tensão ou corrente, sem precisarmos encontrar a EDO e resolvê-la.
Mas na realidade, como vimos nas teorias anteriores, tudo parte de uma EDO de primeira ou segunda ordem. Isso porque a partir dela chegamos nos casos de amortecimento e nas soluções gerais.
A gente só fez algumas deduções e utilizou de técnicas para pular essa etapa de resolver a EDO de maneira clássica, mas se você se sente seguro, pode resolvê-la normalmente, como a gente fez em alguns exercícios até aqui.
Nesse tópico a gente vai ver como resolver a EDO do circuito aplicando Transformada de Laplace.
Solução de Circuitos por Transformada de Laplace
Agora chega de papo. Vamos botar a mão na massa!
Para você ver que funciona, eu peguei o mesmo exemplo da teoria do tópico anterior. Vamos encontrar a tensão para no circuito abaixo, utilizando a Transformada de Laplace para resolvermos a EDO.
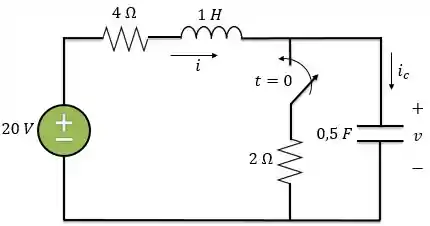
Para isso, vamos seguir alguns passos.
1º PASSO:
Esse passo é praticamente igual para todas as análises de circuitos. A gente precisa determinar nossas condições iniciais.
Em , a chave está aberta e podemos considerar o circuito em regime permanente. Então, podemos considerar o indutor um curto-circuito e o capacitor um circuito aberto.
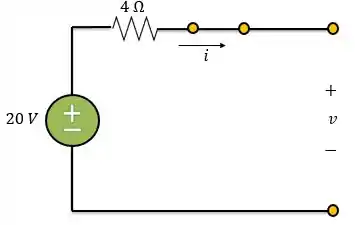
Como circuito está aberto, não há circulação de corrente e, consequentemente, não há queda de tensão no resistor. Logo,
Em a chave é fechada e temos o seguinte circuito:
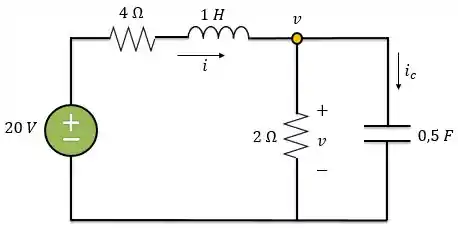
Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que
Como queremos encontrar , ainda precisamos determinar . Como o capacitor está em paralelo com o resistor de , eles possuem a mesma tensão
Sabemos que no capacitor
Logo,
Aplicando LCK ao nó do circuito,
Portanto,
2º PASSO:
Agora, vamos encontrar a EDO que descreve no circuito para
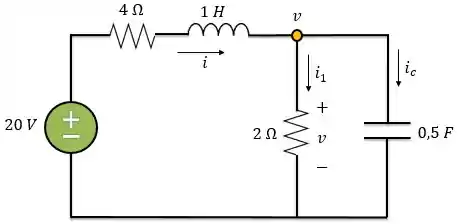
Aplicando LCK ao nó do circuito acima,
Logo,
E aplicando LTK na malha da esquerda,
Como a gente está querendo determinar a tensão , vamos substituir da primeira equação na segunda.
Simplificando,
Arrumando os termos,
Que podemos escrever também desta maneira:
3º PASSO:
Agora que encontramos EDO de segunda ordem não homogênea, precisamos resolvê-la utilizando Transformada de Laplace. Para isso, primeiro precisamos encontrar uma expressão para .
Para relembrar como funciona, vamos aplicar transformada de Laplace em cada termo da EDO:
Quando temos uma constante sempre consideramos ela multiplicada pelo degrau unitário, porque para .
Logo,
Como,
Portanto, a nossa equação transformada é
Substituindo as condições iniciais que encontramos no primeiro passo
Temos,
Simplificando,
Isolando a transformada da tensão,
4º PASSO:
Agora que encontramos a expressão para , vamos utilizar o método de expansão em frações parciais.
Fatorando o polinômio do denominador, temos
Expandindo em frações parciais,
Agora, precisamos determinar as constantes e .
Como a raiz de é zero, para temos
Simplificando,
Vamos seguir o mesmo processo para encontrarmos .
Como a raiz de é , temos:
Simplificando,
E para
Simplificando,
Substituindo o valor de cada constante, temos que
5º PASSO:
Agora que encontramos a expressão para em frações parciais, vamos aplicar a Transformada inversa de Laplace:
Mais abaixo, eu vou fazer uma tabela com as funções mais usadas e suas respectivas Transformadas de Laplace, para você dar aquela relembrada. Mas, adiantando, sabendo que
Portanto,
A gente sempre multiplica cada termo da equação pelo degrau unitário , para deixar claro que a expressão é válida apenas para .
A gente também pode escrever a resposta acima da seguinte maneira:
Pronto! Missão cumprida.
Vamos relembrar os passos:
- Determinar as condições iniciais e ;
- Encontrar a EDO que descreve no circuito para , aplicando a LCK ou LTK no circuito;
- Aplicar a Transformada de Laplace na EDO para encontrar uma expressão para
- Utilizar o método de expansão em frações parciais, para partir em somas de parcelas mais simples;
- Aplicar a Transformada inversa de Laplace
Seguindo esses passos não tem erro. Abaixo tem a tabela com as funções mais usadas e suas respectivas Transformadas de Laplace.

Agora é praticar! Separei exercícios espertos para você. 😉