Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 5

Se R 1 = R 2 = 0.5 Ω e R 3 = 0.01 Ω no Prob. 15.4, calcule H ( s ) , a frequência ω 0 na qual o pico da amplitude e a fase zero ocorrem e o módulo de H em ω 0 .

Passo 1

Eaeee!! Beleza?

Bom, o circuito que a questão tá falando é esse aqui:

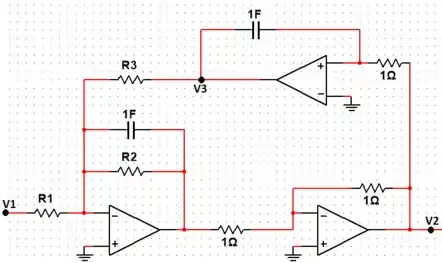
Passo 2

Na questão anterior, descobrimos que H ( s ) é dado por:

H s = s R 1 s 2 + s R 2 + 1 R 3

Assim, substituindo os valores das resistências, temos:

H s = s 0.5 s 2 + s 0.5 + 1 0.01 ∴

H s = 2 s s 2 + 2 s + 100

Passo 3

Percebemos que H ( s ) tem o formato de:

K s s 2 + B s + ω 0 2

Logo, temos que:

K = 2

B = 2

ω 0 = 10

Assim, fazendo s = j ω , temos:

H j ω = 2 j ω j ω 2 + 2 j ω + 100 ∴

H j ω = 1 1 + j ω 2 - 50 ω

Passo 4

Dessa forma, para a amplitude máxima, temos:

ω 0 2 - 50 ω 0 = 0 ∴

ω 0 2 - 100 2 ω 0 = 0 ∴

ω 0 = 10

Passo 5

O módulo de H em ω 0 é dado por:

H j ω m á x = K B = 2 2 = 1

Tranquilo?? Let’s go to one more question (respeita o inglês do pae)!!

Resposta

H s = 2 s s 2 + 2 s + 100

ω 0 = 10

H j ω m á x = 1

Exercícios de Livros Relacionados

Simplifique o seguinte: f t = 5 cos ⁡ ( 2 t + 15 ° ) - 4 sen ⁡ ( 2 t - 30 ° ) g t = 8 sen ⁡ t + 4 cos ⁡ t + 50 ° h t = ∫ 0 t 10 cos ⁡ 40 t + 4 sen ⁡ 40 t d t
Um circuito linear tem corrente de entrada 7,5 cos ⁡ ( 10 t + 30 ° )A e tensão de saída 120 cos ⁡ ( 10 t + 75 ° )V . Determine a impedância associada.
Simplifique o seguinte: f t = 5 cos ⁡ ( 2 t + 15 ° ) - 4 sen ⁡ ( 2 t - 30 ° ) g t = 8 sen ⁡ t + 4 cos ⁡ t + 50 ° h t = ∫ 0 t 10 cos ⁡ 40 t + 4 sen ⁡ 40 t d t
A equação de malha para um circuito R L C série é d i d t + 2 i + ∫ - ∞ t id t = cos ⁡ ( 2 t )A Supondo que o valor da integral em t = - ∞ seja zero, determine i ( t ) usando o método de fasores.
Determine v ( t ) nas seguintes equações integro-diferenciais usando o método de fasores: v t + ∫ v d t = 10 cos ⁡ t d v d t + 5 v t + 4 ∫ v d t = 20 s e n ( 4 t + 10 ° )