Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 45
Considere o circuito mostrado na Figura e determine o valor da potência média absorvida pelo resistor de .
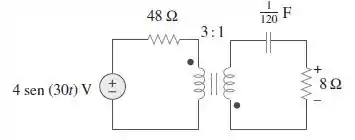
Passo 1
Pessoal, a primeira coisa é transformar os componentes do domínio do tempo para o domínio da frequência:
Aplicando a lei das malhas na malha da esquerda, temos:
Similarmente, aplicando a lei das malhas na malha da direita,
Nos terminais dos transformadores,
Passo 2
Substituindo as equações e na equação ,
Substituindo a equação na equação de cima, temos:
Assim,
Passo 3
Desse modo, a potência absorvida pelo resistor de é igual a:
Resposta
A potência absorvida pelo resistor é igual a:
Exercícios de Livros Relacionados
Um autotransformador com uma derivação de 40 % é alimentado por uma fonte de 400V ,60H z e é usado para operação de redução de tensão. Uma carga é 5 k V A operando com fator de potência unitário é con
No circuito com autotransformador da Figura 13.134 , demonstre que Z e n t = 1 + N 1 N 2 2 Z L
No circuito da Figura 13.132 , Z L é ajustada até a máxima potência media ser liberada para Z L . Determinar Z L e a máxima potência média transferida para ela. Considere N 1 = 600 espiras e N 2 = 200
No circuito do transformador ideal da Figura 13.133 , determine a potência média liberada para a carga.
No autotransformador ideal da Figura 13.131 , calcule I 1 ,I 2 e I 0 . Determine a potência média liberada para a carga.