Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 65
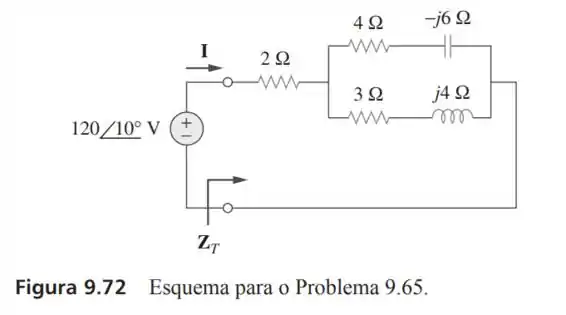
65- Determine e no circuito da Figura .
Passo 1
A impedância total desse circuito será a a impedância em paralelo das impedâncias de e em série com a de nos dando a impedância igual a:
Transformando em fasor:
Transformando para a complexa e depois para um fasor nós teremos
Passo 2
Então a corrente total será:
Pois a corrente total irá fluir de acordo com a impedância total
Resposta
Exercícios de Livros Relacionados
a) Mostre que, a uma dada frequência ω , os circuitos na Figura P9.20(a) e (b) terão a mesma impedância entre os terminais a,b se R 2 = 1 + ω 2 R 1 2 C 1 2 ω 2 R 1 2 C 1 2 C 2 = C 1 1 + ω 2 R 1 2 C 1
a) Usando os valores dos componentes do apêndice H, combine, pelo menos, um resistor e um indutor em paralelo para criar uma impedância de 40 + j20 Ω a uma frequência de 5.000 rad/s. (Sugestão: use os
Determine Zab para o circuito mostrado na Figura P9.42.
O valor de k no circuito da Figura P9.74 é ajustado de modo que Zab seja puramente resistiva quando v = 4 krad/s. Determine Zab.
Mostre em:a) que a regra de divisão de tensão, V = Z 2 Z 1 + Z 2 V g b) que regra de divisão de corrente, I = Y 2 Y 1 + Y 2 I g = Z 1 Z 1 + Z 2 I g São validas, onde Z 1 = 1 Y 1 e Z 2 = 1 Y 2 ,