Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 69
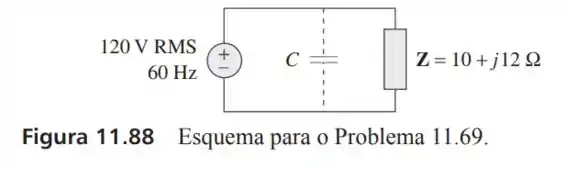
69- Consulte o circuito mostrada na Figura
Qual é o fator de potência?
Qual é a potência média dissipada?
Qual é o valor da capacitância que fornecerá um fator de potência unitário quando conectado a carga?
Passo 1
O fator de potência depende única e exclusivamente da impedância. E para isso vamos calcular o ângulo de fase provocado por ela:
E o fator de potência será calculado por:
Passo 2
Para calcular a potência total já sabendo que essa fonte é .
Sabendo que para uma reatância indutiva.
Então:
Passo 3
Na letra nós queremos zerar a potência reativa e para podermos calcular esse capacitor nós utilizamos a seguinte fórmula:
Resposta
Exercícios de Livros Relacionados
39- Um motor C A com impedância Z L = 4.2 + j 3.6Ω é alimentado por uma fonte de 220V ,60H z . ( a ) Determine F P ,P e Q . ( b ) Determine o capacitor necessário para ser conectado em paralelo com o
a) Se N 1 for igual a 1.000 espiras, quantas espiras deve ter o enrolamento N 2 do transformador ideal, no circuito apresentado na Figura P10.64, para que seja fornecida máxima potência média à carga
a) Determine a impedância de carga para o circuito da Figura P10.41 para a máxima transferência de potência média à carga, se ω = 8k r a d / s .b) Determine a máxima potência média fornecida à carga n
As três cargas do circuito da Figura P10.30 podem ser descritas da seguinte forma: a carga 1 é um resistor de 240Ω em série com uma reatância indutiva de 70Ω ; a carga 2 é uma reatância capacitiva de
a) Determine as seis correntes de ramo I a - I f no circuito da Figura P10.36.b) Determine a potência complexa em cada ramo do circuito.c) Confirme seus cálculos verificando se a potência média fornec